yektasimsek 03:53 28 Haz 2013 #1 
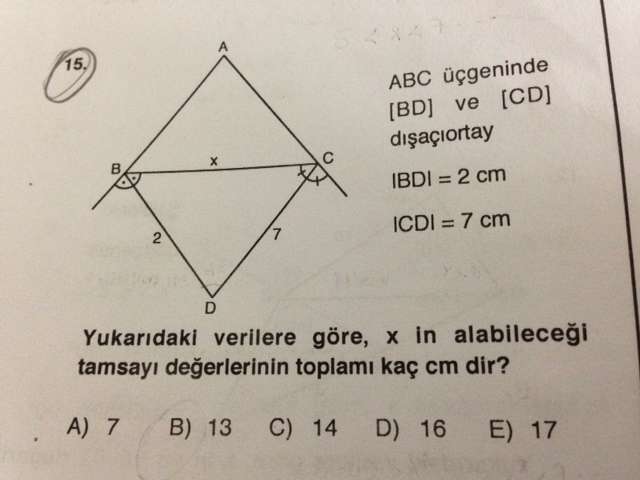
Üstteki soruyu 13 buluyorum fakat 7 diyor.
Burada neye göre değerlendiriyoruz?
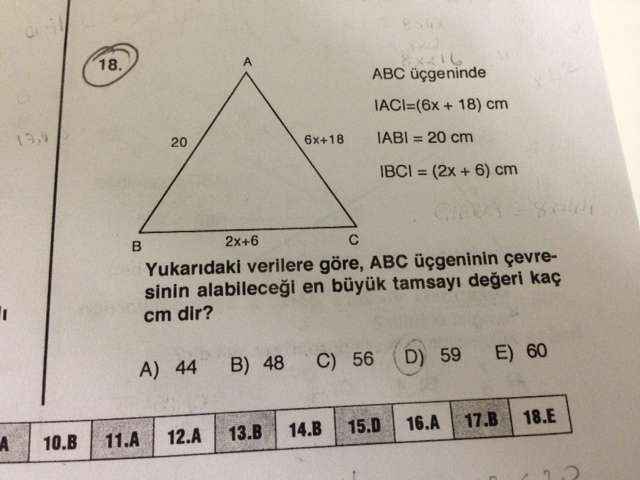
Bunu da 59 buldum fakat cevap 60'mış.
Şimdiden teşekkürler.
svsmumcu26 10:24 28 Haz 2013 #2
1.
dışaçıortay başlığı altında bakarsanız m(bdc)=90-m(bac) olduğundan her durumda dar olacaktır.o dış açıortayların her birisi geniş olsa dahi üçgenin içinde kalanlar dar olacaktır.Burada şöyle bir şekilde çözüm yapabiliriz m(d)<90* diye x^2<49+4 => x^2<53 x<√53 bulunur. => x≤7 diyebiliriz yani.bir de farklarından da üçgen eşitsizliğinden dolayı büyük olmalıdır 5<x≤7 , x=6 ve 7 için 13 bulunur.ama bir başka pisagor eşitsizliğini başka bir kenarda uygularsak
49<x²+4
45<x²
neden sadece 7yi alabileceğimizi görmüş oluruz.
2.
Buna kahvaltıdan sonra bakayım kağıt kalem filan da yok yanımda.
3.
burada doğru buldunuz galiba (en azından bu kafayla ben de öyle buluyorum.)
59 oluyor.
4x+12<20<8x+24
4x<8 , 8x<16 , 8x+44<60 maksimum 59.
dışaçıortay başlığı altında bakarsanız m(bdc)=90-m(bac) olduğundan her durumda dar olacaktır.o dış açıortayların her birisi geniş olsa dahi üçgenin içinde kalanlar dar olacaktır.Burada şöyle bir şekilde çözüm yapabiliriz m(d)<90* diye x^2<49+4 => x^2<53 x<√53 bulunur. => x≤7 diyebiliriz yani.bir de farklarından da üçgen eşitsizliğinden dolayı büyük olmalıdır 5<x≤7 , x=6 ve 7 için 13 bulunur.ama bir başka pisagor eşitsizliğini başka bir kenarda uygularsak
49<x²+4
45<x²
neden sadece 7yi alabileceğimizi görmüş oluruz.
2.
Buna kahvaltıdan sonra bakayım kağıt kalem filan da yok yanımda.
3.
burada doğru buldunuz galiba (en azından bu kafayla ben de öyle buluyorum.)
59 oluyor.
4x+12<20<8x+24
4x<8 , 8x<16 , 8x+44<60 maksimum 59.
svsmumcu26 01:35 30 Haz 2013 #3
2.
bunu unutmuşum şimdi yazayım.
iki kenar uzunluğu belli bir üçgenin üçüncü kenarına inen yüksekliğin boyu en fazla yan kenarlardan kısa olanın boyu kadardır.
bu teoreme göre 2. yargının çizilemeyeceğini direkt görebiliriz.
bunu unutmuşum şimdi yazayım.
iki kenar uzunluğu belli bir üçgenin üçüncü kenarına inen yüksekliğin boyu en fazla yan kenarlardan kısa olanın boyu kadardır.
bu teoreme göre 2. yargının çizilemeyeceğini direkt görebiliriz.