gereksizyorumcu 00:56 19 Eyl 2012 #4
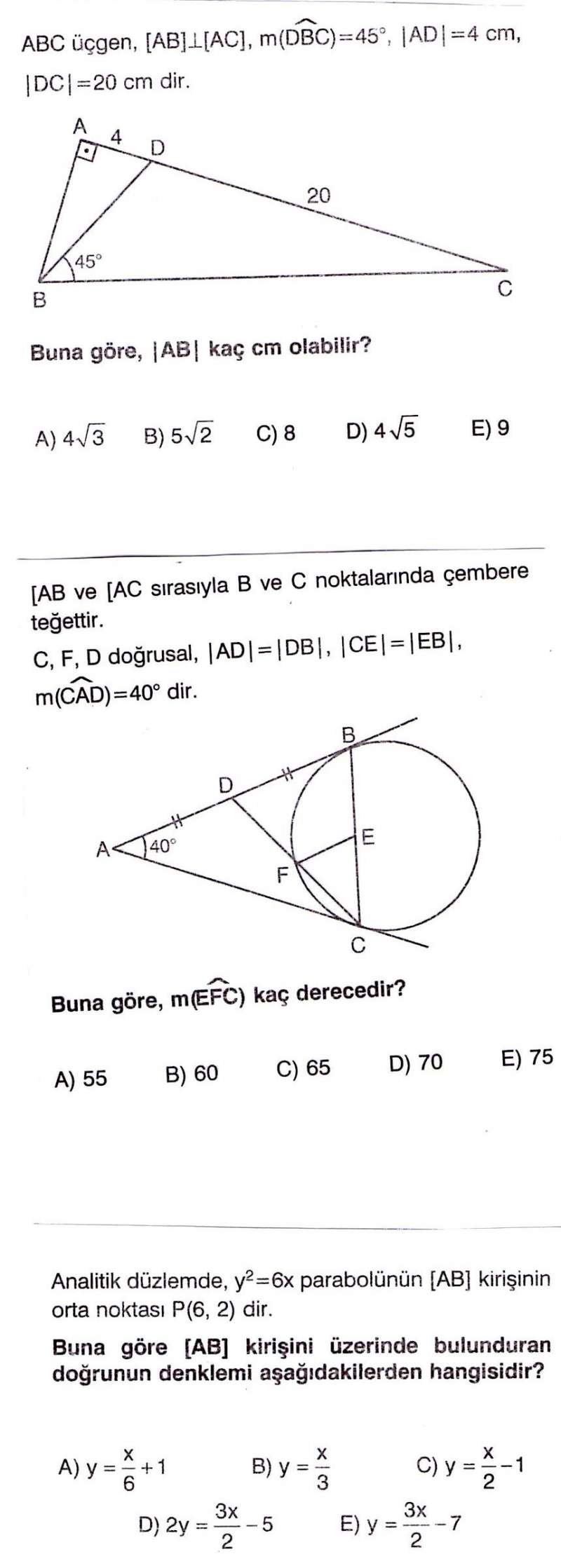
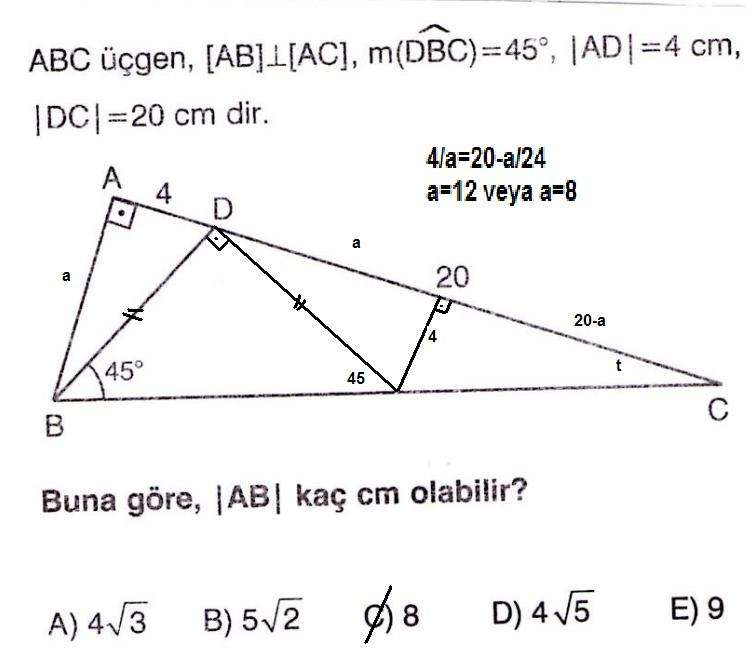
güzel çözümmüş bravo
ben de BD ye x dedikten sonra a dediğiniz yere √(x²-16) , BC ye √2((x²+80)/x) (kuvvetten
)
diyip denklem çözmüştüm , x²=t dönüşümü yapınca da denklemde t=160 veya t=80 çıkıyordu buradan BD=4√5 veya 4√10 ya da a=8 veya 12
ama daha iyi çözüm bulunacaktır diye yazmamıştım
ben de BD ye x dedikten sonra a dediğiniz yere √(x²-16) , BC ye √2((x²+80)/x) (kuvvetten
)diyip denklem çözmüştüm , x²=t dönüşümü yapınca da denklemde t=160 veya t=80 çıkıyordu buradan BD=4√5 veya 4√10 ya da a=8 veya 12
ama daha iyi çözüm bulunacaktır diye yazmamıştım
gereksizyorumcu 01:04 19 Eyl 2012 #6 
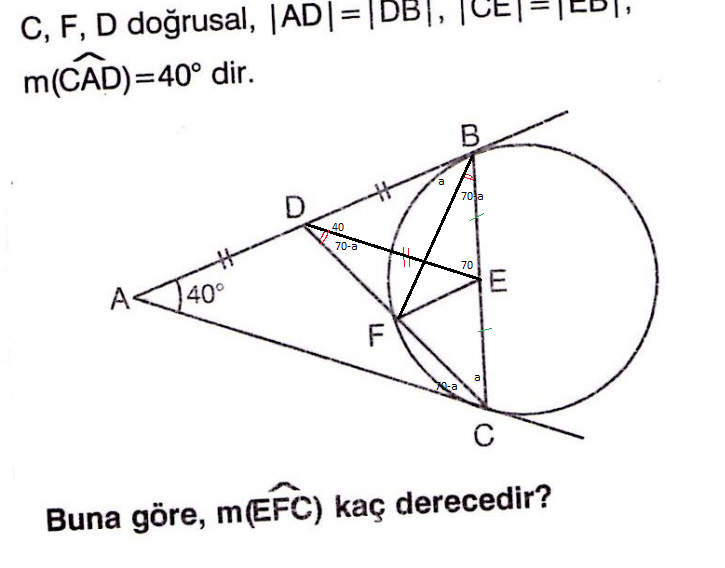
kırmızı ile işaretlenmiş iki açı birbirine eşit öyleyse FEBD çemberseldir ve sorulan açı da ters taraftaki iç açıya yani DBE ye eşit olur 70º bulunur
kırmızı ile işaretlenmiş iki açı birbirine eşit öyleyse FEBD çemberseldir ve sorulan açı da ters taraftaki iç açıya yani DBE ye eşit olur 70º bulunur
güzel çözümmüş bravo
teşekkürler.
gereksizyorumcu 02:22 19 Eyl 2012 #8 hocam yarım saattir ECF açısını hesaplamaya çalışıyorum onu bulma imkanımız var mı
)sinüs teoremini yazarız
((sin70)/2)/sina=((sin40)/2)/sin(70-a)
düzenlenirse
sin70/sin40=sina/sin(70-a) , bunu da wolframa çözdürünce 42.184º gibi bişey çıkıyor sanırım. yani hoş bi açı değil boşuna uğraşmayalım.
çok şartsa onu da buluruz (daha doğrusu buldururuz )
sinüs teoremini yazarız
((sin70)/2)/sina=((sin40)/2)/sin(70-a)
düzenlenirse
sin70/sin40=sina/sin(70-a) , bunu da wolframa çözdürünce 42.184º gibi bişey çıkıyor sanırım. yani hoş bi açı değil boşuna uğraşmayalım.
)sinüs teoremini yazarız
((sin70)/2)/sina=((sin40)/2)/sin(70-a)
düzenlenirse
sin70/sin40=sina/sin(70-a) , bunu da wolframa çözdürünce 42.184º gibi bişey çıkıyor sanırım. yani hoş bi açı değil boşuna uğraşmayalım.
MatematikciFM 03:45 19 Eyl 2012 #10
3. soru için şöyle bir genelleme yapmaya çalışayım.
y²=kx parabolünün, eğimi m olan kirişlerinin orta noktaları y=b doğrusu üzerinde olsun.
O zaman
m=k/2b
dir.
Soruda
k=6, b=2 olduğundan
m=6/(2.2)=3/2
Eğimi m olan ve (6,2) noktasından geçen doğrunun denklemi y=(3x/2)-7 dir.
y²=kx parabolünün, eğimi m olan kirişlerinin orta noktaları y=b doğrusu üzerinde olsun.
O zaman
m=k/2b
dir.
Soruda
k=6, b=2 olduğundan
m=6/(2.2)=3/2
Eğimi m olan ve (6,2) noktasından geçen doğrunun denklemi y=(3x/2)-7 dir.