Karmaşık Sayıların Kutupsal Gösterimi - Karmaşık Sayılarda Argüment

Karmaşık Sayıların Kutupsal Biçimde Gösterimi - Karmaşık Sayılarda Argüment


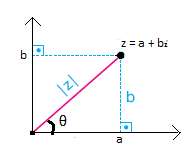
r =|Z|=|OZ|= √a²+b²

reel sayısına Z nin mutlak değeri (modülü) denir.

a) |z|=|z|=|-z|

b) |z₁.z₂|=|z₁|.|z₂|

c) |z|.|z| = |z|²

d) |z₁ⁿ|= (|z₁|)ⁿ

e)


θ sayısına z karmaşık sayısının esas argümenti denir ve Arg(z) = θ ile gösterilir. Yukarıdaki dik üçgende;





olduğuna göre;





biçiminde yazılabilir. Buna z'nin kutupsal biçimi denir.

Kutupsal Gösterimin Özellikleri

z₁ =|z₁|(Cosθ + i.Sinθ) ve z₂ =|z₂|(Cosα + iSinα) ise:

1) -z₁ =|z₁|. [Cos(∏+θ) + iSin(∏+θ)]

2) z₁ =|z₁|. [Cos(2.∏-θ) + iSin(2.∏-θ)]

3) z₁ . z₂ =|z₁|.|z₂|[Cos(θ+α) + iSin(θ+α)]

4) z₁ⁿ =|z₁|ⁿ . (Cosnθ + iSinnθ)

Karmaşık Sayıların Kökleri

5)

6)

Buna göre z nin kare kökleri:





Karmaşık Sayıların Geometrik Özellikleri

1) |z - (a+b)i|= r denklemi analitik düzlemde merkezi M(a,b) ve yarıçapı r olan çember denklemidir.

2) |z - (a+b)i|< r ifadesi merkezi M(a,b) ve yarı çapı r olan çemberin iç bölgesidir.

3) |z - (a+b)i|> r ifadesi merkezi M(a,b) ve yarıçapı r olan çemberin dış bölgesidir.

4) |z₁+z₂|≤|z₁|+|z₂|

ÖRNEK 1:

z=1+cos80+isin80

karmaşık sayısının esas argümentini bulunuz.

ÇÖZÜM 1:

z=1+2cos²40-1+i.2sin40.cos40

z=2cos40(cos40+sin40)

|z|=2cos40

Arg(z)=40

ÖRNEK 2:


Arg(z+3)=pi/4

Arg(z-2+i)=3pi/4

ise z nedir ?

ÇÖZÜM 2:

z=x+yi yazalım

Arg(x+yi+3)=pi/4
Arg(x+yi-2+i)=3pi/4

tan(pi/4)=y/(x+3)=1
tan(3pi/4)=(y+1)/(x-2)=-1

y-x=3
y+x=1

y=2,x=-1

z=-1+2i bulunur.

Karmaşık Sayı Formülleri
Tüm Etiketler