Binom Açılımının Özellikleri

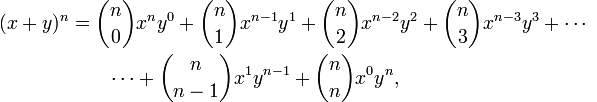
(x+y)ⁿ açılımında:

1) n+1 tane terim vardır.
2) Her terimdeki üsler toplamı n dir.
3) Açılım, x in azalan kuvvetlerine göre sıralandığında, baştan r+1 inci terim C(n,r).x^n-r.y^r dir.
4) Katsayılar toplamı; x ve y terimlerinin tüm katsayıları toplamı bulunması için bütün değişkenlere (x,y,..) 1 verilerek hesaplanır.
5) Sabit terim; sabit terim bu açılımda xli veyli terim bulunmayan terime denir. BU terimi bulmak için bütün değişkenlere 0 verilir.

(a+b)^2 (a-b)^2 (a+b)^3 (a-b)^3 (a+b)^4 (a-b)^4 (a+b)^5 (a-b)^5

(a + b)² = a² + 2ab + b²

(a - b)² = a² - 2ab + b²


(a + b)³ = a³ + 3a²b + 3ab² + b³

(a - b)³ = a³ - 3a²b + 3ab² - b³



(a + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴

(a - b)⁴ = a⁴ - 4a³b + 6a²b² - 4ab³ + b⁴



(a + b)⁵ = a⁵ + 5a⁴b + 10a³b² + 10a²b³ + 5ab⁴ + b⁵

(a - b)⁵ = a⁵ - 5a⁴b + 10a³b² - 10a²b³ + 5ab⁴ - b⁵

Ama bir üç terimlinin açılımı binom açılımı değildir. Binom iki terimli demektir. Aklında olsun...

Örnek 1

(3x-2y)⁵ ifadesinin açılımında kaç tane terim vardır?

Çözüm 1

Formülden yararlanalım, (x+y)ⁿ açılımında n+1 tane terim vardır.
Soruda n=5 olarak verilmiş, 5+1=6 tane terimi vardır.

Örnek 2




ifadesinin açılımındaki kat sayılar toplamı kaçtır?


Çözüm 2

Katsayılar toplamı için x=1 yazalım,

ÖRNEK 3:


(x+2y)³

ifadesinin açılımını yapınız.

ÇÖZÜM 3:

ilk olarak (x+2y)³ açılımındaki terimlerin çarpanlarını x'in azalan, y'nin artan kuvvetlerine göre sıralayalım. Sonra katsayılarını bulalım.

(x+2y)³=?x³+?x²(2y)¹+?x¹(2y)²+?(2y)³

Şimdi de katsayıları yani (?) yerine gelecek sayıları bulalım

sırayla;

C(3,0),C(3,1),C(3,2),C(3,3) olur.

Toparlarsak;

(x+2y)³=C(3,0).x³+C(3,1).x²2y+C(3,2).x.(2y)²+C(3,3).(2y)³

(x+2y)³=x³+6x²y+12xy²+8y³ olur.

Binom Açılımı Soruları
Tüm Etiketler