8. Sınıf SBS Matematik Soruları ve Çözümleri - 9 Haziran 2012

gökberk 01:35 11 Haz 2012 #1

Soruda istenen 8,1.10⁵ tonu, 81.10⁴ olarak yazmak işlem kolaylığı sağlar.

Oran orantı kullanalım,

1 ton kağıt 18 ağaç ise,
x ton kağıt 81.10⁴ ağaç.

Doğru orantı olduğundan,
18x=81.10⁴
x=81.10⁴/18
x=9.10⁴/2
x=4,5.10⁴ olarak bulunur.

Bütün sayıları kök içerisine alalım,
2√10=√40
√17
3√3=√27

Şimdi kökleri görmeden sıralama yapabiliriz.

√17<√27<√40

Şıklara uyarlayalım,

√17<3√3<2√10

Her katta yarıçapı 2 ile çarptığımızdan, 2'nin kuvveti bir artar,
1. kat, 2³
2. kat 2⁴
3. kat 2⁵
4. kat 2⁶
5. kat 2⁷ olacaktır.

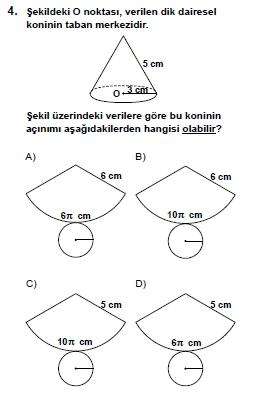
Açılımlarda anadoğru uzunluğu 5cm olmalıdır. Yani cevap C veya D şıkkıdır.
Daire yayının uzunluğu ise, tabanın çevresine eşittir.
Taban çevresi=2∏r=2.3.∏=6∏

Öyleyse cevap D şıkkıdır.

Karenin toplam alanı 9a²'dir.
Belirlenen her bir bölgenin alanı 4b²'dir.
x tane bölge belirlenmiş olsun, toplam belirli alan, x.4b² olacaktır.

Geri kalan alan, (3a-4b).(3a+4b)=9a²-16b² olarak verilmiş.
9a²-x.4b²=9a²-16b²
x.4b²=16b²
x=4 bulunur.

Üçüncü kenar uzunluğu x olsun.
17-10<x<17+10
7<x<27 olmalıdır.

x'in en büyük değeri olan 26 için çevre uzunluğu, 17+10+26=53 olur.
x'in en küçük değeri 8 için çevre uzunluğu, 17+10+8=35 olur.
Çevre uzunluğu [35,53] aralığında olmalıdır. Şıklardaki 40 bu aralığa uygundur.

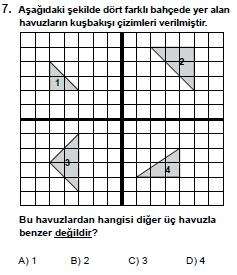
1 numaralı üçgenin kenar uzunlukları, 2-2-2√2
2 numaralı üçgenin kenar uzunlukları, 3-3-3√2
3 numaralı üçgenin kenar uzunlukları, 2√2-2√2-4
4 numaralı üçgenin kenar uzunluklar, 2-3-√13'dür.

1,2,3 numaralı üçgenlerde bir kenar, diğer iki kenarın √2 katıdır. (45-45-90 üçgeni). 4 numaralı üçgende bu benzerlik görülmemekte.

İlk sınavda aldığı puan x olsun.
2x-4≥50 olmalıdır.
2x≥54
x≥27 olmalı.
x en küçük 27 olabilir.

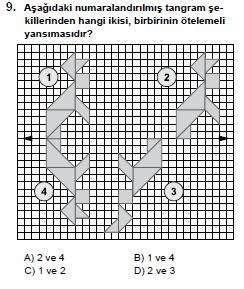
4 numaralı şeklin önce doğruya göre yansıması alınıp, sonra sağa doğru ötelenerek 2 numaralı şekil elde edilmiştir. Cevap 2 ve 4 olmalıdır.

Verilen devredenleri biraz daha açarak yazalım,

0,45=0,454...
0,452=0,452...

Şıklardan 0,453 bizden istenen aralıkta bulunur.

gökberk 02:00 11 Haz 2012 #2

Kapaktan sandığa bir dikme indirerek dik üçgen oluşturalım
Verilen 30 derecelik açının sinüsünden yararlanalım.
Sinüs=Karşı Dik Kenar / Hipotenüs
Karşı kenar x olsun,
sin30=1/2
x/210=1/2
x=105 bulunur.

Ceren'in boyu için bu uzunluğa sandığın yerden yüksekliğini ekleyelim,
105+46=151cm olacaktır.

Hacim=Taban Alanı x Yükseklik olduğundan, yüksekliği yarıya indirmek hacmin de yarıya inmesini sağlar.
Yükseklik 6cm azalırsa yarıya inmiş olur.
Cevap D şıkkı olmalıdır.

4 tane yüz boyanmıştır.
Bizden istenen diğer ayrıt x olsun.
30.4.x=1680
120x=1680
x=14 olarak bulunur.

Küpün bir ayrıt uzunluğu 2x olsun.
Silindirin yüksekliği 2x, yarıçapı x olur.
Küpün hacmi, (2x)³=8x³
Silindirin hacmi, 3.x².2x=6x³ olur.
İkisinin oranı, 6x³/8x³=3/4 olacaktır.

Top sayıları eşit olmalıdır, en az olanda eşitleyelim, yani her birinden 8 tane olmalı.
3 tane kırmızı, 1 tane mavi, 4 tane siyah top çıkartırsak eşitlenir.
3+1+4=8 top çıkartılmalıdır.

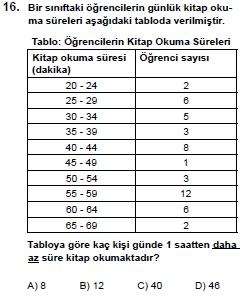
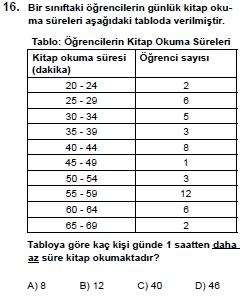
60-64 ve 65-69 aralıkları dışındaki öğrencileri toplamalıyız.
2+6+5+3+8+1+3+12=40

İlk üç yoldan birini C(3,1)=3 farklı şekilde seçer.
Daha sonra karşısına çıkan ikili yollardan birini de C(2,1)=2 farklı şekilde seçer.
Toplam 3.2=6 farklı seçim yapabilir.
Bu seçimlerden yalnız birinin sonunda kaplumbağa vardır.
1/6 ihtimal ile karşılaşırlar.

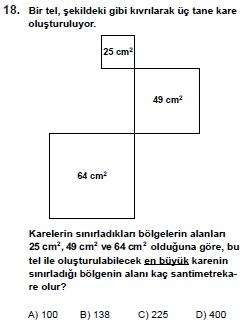
İlk karenin bir kenar uzunluğu √25=5cm
İkinci karenin bir kenar uzunluğu √49=7cm
Üçüncü karenin bir kenar uzunluğu √64=8cm'dir.
Yeni oluşturulacak karenin bir kenar uzunluğu en fazla 5+7+8=20cm olabilir.
Alanı ise 20.20=400cm² olabilir.

Doğru cevaplanan soru sayısı x olsun,
3x puan alınmıştır.
Yanlış cevaplanan soru sayısı 5-x olacaktır.
2.(5-x) puan kaybedilmiştir.

3x-2(5-x)=10
3x+2x-10=10
5x=20
x=4 olarak bulunur.

y yalnız bırakıldığında x'in katsayısı eğimi verir.

y=bx+3 ve y=cx doğruları paralel, eğimleri eşit, olduğundan b=c olmalıdır.
Sola yatık doğruların eğimi negatif, sağa yatık doğruların eğimi pozitiftir.
Bu durumda a<0, b=c>0 olmalıdır.
a<b=c eşitsizliği yazılabilir.
A şıkkı isteneni sağlar.