Aşağıdaki soruları çözemedim yardımcı olursanız çok sevinirim
https://i.hizliresim.com/WqbBym.jpg Soru 1
https://i.hizliresim.com/jgB0OW.jpg Soru 2
https://i.hizliresim.com/WqbBym.jpg Soru 1
https://i.hizliresim.com/jgB0OW.jpg Soru 2
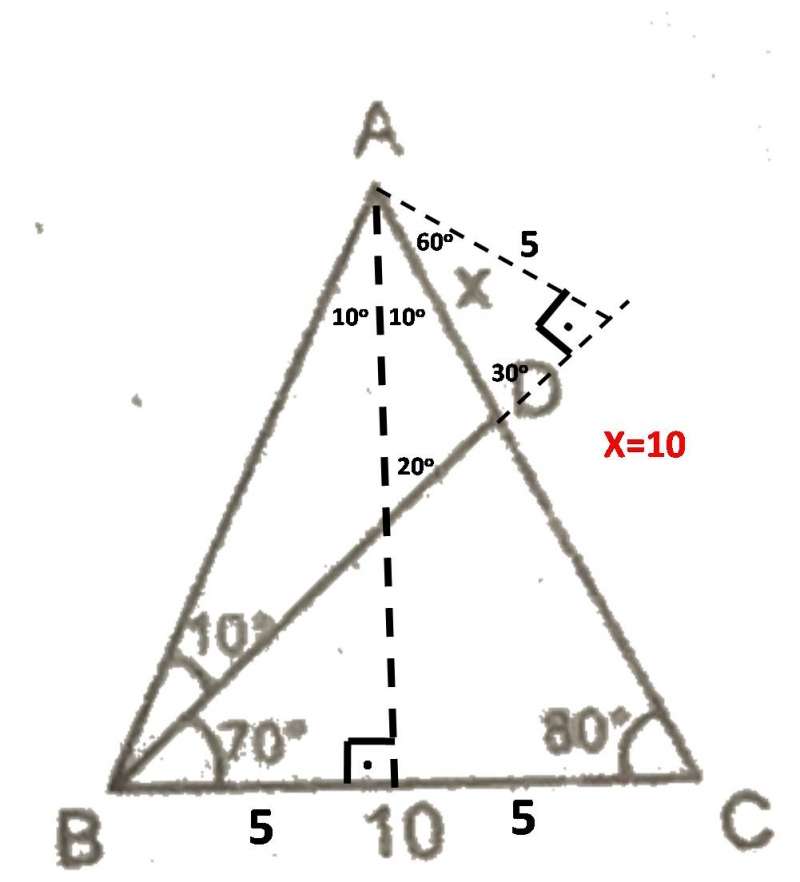
1) İlk olarak A köşesinden |BC| kenarına bir dik çizerek ikizkenar ABC üçgeninin |BC| kenarını eşit iki parçaya ve A açısını 10 derecelik iki parçaya bölelim. |BD| doğru parçasını uzatarak bu parçaya A köşesinden bir dikme indirirsek oluşan iki dik üçgen birbirine eş üçgenler olacaktır.
Açıları doğru bir şekilde yerleştirdiğimizde x uzunluğunun oluan 30-60-90 üçgeninden 10 olarak bulunacağı görülebilir.
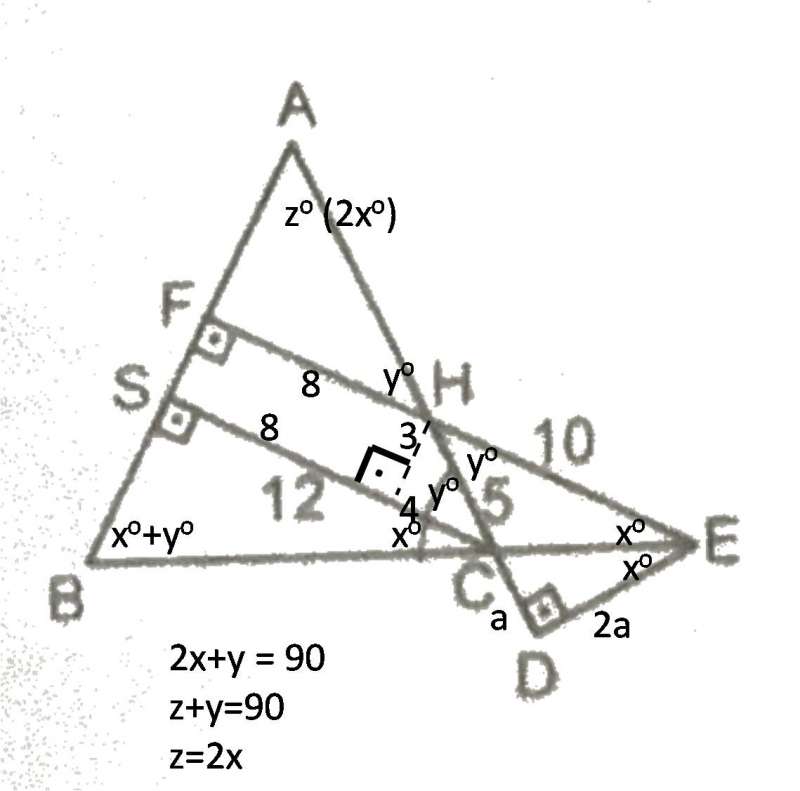
2) Verilen üçgene |AB|=|AC| olması sebebiyle ABC açısı ve BCA açısı birbirine eşittir. BCS açısına x ve SCH açısına y dersek ABC açısı x+y olacaktır. Bu durumda BCS üçgeninde açılar toplamından 2x+y = 90 derecedir. BAD açısının da 2x olması gerekir.
DEH üçgeninde açılar uygun şekilde yerleştirilirse |EC| doğru parçasının bir açıortay olduğu görülecektir. İç açıortay teoremine göre; olacağından |CD|=a dersek |DE|=2a olacaktır.
DEH üçgeninde pisagor uygulanırsa; 4a² + (5+a)² = 100 ise 5a² + 10a - 75 = 0 olacaktır.
İfade düzenlenirse; (5a + 25)(a-3)=0 olacaktır ve a={-5,3} bulunur. u durumda a=3 olacaktır.
H noktasından |CS| kenarına bir dik indirildiğinde DEH üçgenine benzer bir üçgen elde edilir. Buradan |FH|=8 olarak bulunur.
Açıları doğru bir şekilde yerleştirdiğimizde x uzunluğunun oluan 30-60-90 üçgeninden 10 olarak bulunacağı görülebilir.

2) Verilen üçgene |AB|=|AC| olması sebebiyle ABC açısı ve BCA açısı birbirine eşittir. BCS açısına x ve SCH açısına y dersek ABC açısı x+y olacaktır. Bu durumda BCS üçgeninde açılar toplamından 2x+y = 90 derecedir. BAD açısının da 2x olması gerekir.
DEH üçgeninde açılar uygun şekilde yerleştirilirse |EC| doğru parçasının bir açıortay olduğu görülecektir. İç açıortay teoremine göre;
|DE|
10
=
|CD|
5
DEH üçgeninde pisagor uygulanırsa; 4a² + (5+a)² = 100 ise 5a² + 10a - 75 = 0 olacaktır.
İfade düzenlenirse; (5a + 25)(a-3)=0 olacaktır ve a={-5,3} bulunur. u durumda a=3 olacaktır.
H noktasından |CS| kenarına bir dik indirildiğinde DEH üçgenine benzer bir üçgen elde edilir. Buradan |FH|=8 olarak bulunur.

