1)
lim
x->sonsuz (3x+ex)2/x ifadesinin değeri kaçtır Cevap 9
2)
ABC dik üçgen AB dik BC m(DAC)=2m(DAB) 5|BD|=2|DC|
Buna göre AD/AC oranı kaçtır 4/5
lim
x->sonsuz (3x+ex)2/x ifadesinin değeri kaçtır Cevap 9
2)
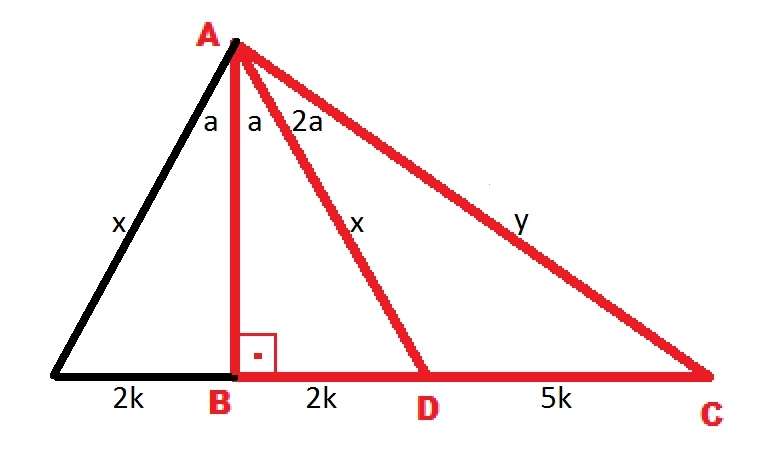
ABC dik üçgen AB dik BC m(DAC)=2m(DAB) 5|BD|=2|DC|
Buna göre AD/AC oranı kaçtır 4/5
1) Verilen limit değerini bulmak için öncelikle doğal logaritmasını almamız gerekmekte;
y=(3x+ex)2/x dersek;
lny=ln(3x+ex)2/x=(2/x).ln(3x+ex) olacaktır. Ayrıca limit özelliklerinden biri olan;
lim lny=ln limy özelliğini kullanırsak;
Bu durumda limitte ∞/∞ belirsizliği söz konusu olacaktır. Pay ve paydanın türevini alarak L-Hospital kuralı uygularsak;
olur.
Burada da yine ∞/∞ belirsizliği söz konusudur. Ancak 3x ifadeleri daha büyük olduğu için katsayılarını oranlarsak limit 2.ln3=ln9 olarak hesaplanır. Bu durumda ln limy=ln9 ise; limy=9 olacaktır.
y=(3x+ex)2/x dersek;
lny=ln(3x+ex)2/x=(2/x).ln(3x+ex) olacaktır. Ayrıca limit özelliklerinden biri olan;
lim lny=ln limy özelliğini kullanırsak;
ln
lim
x→∞
y=
lim
x→∞
(2/x).ln(3x+ex) olur.
Bu durumda limitte ∞/∞ belirsizliği söz konusu olacaktır. Pay ve paydanın türevini alarak L-Hospital kuralı uygularsak;
ln
lim
x→∞
y=
lim
x→∞
(3x.ln3+ex)
2
3x+ex
Burada da yine ∞/∞ belirsizliği söz konusudur. Ancak 3x ifadeleri daha büyük olduğu için katsayılarını oranlarsak limit 2.ln3=ln9 olarak hesaplanır. Bu durumda ln limy=ln9 ise; limy=9 olacaktır.
Çok sağolun enesemre ve savaş
Süleyman Oymak 23:06 05 Haz 2015 #4 2.
ABC dik üçgen AB dik BC m(DAC)=2m(DAB) 5|BD|=2|DC|
Buna göre AD/AC oranı kaçtır 4/5
ABC dik üçgen AB dik BC m(DAC)=2m(DAB) 5|BD|=2|DC|
Buna göre AD/AC oranı kaçtır 4/5
Çok sağolun hocam