Nasılyaniya 13:50 04 Eyl 2014 #1 1) z1=6cis20
z2=8cis140 karmaşık sayıları arasındaki uzaklık kaç br? 2√37
2) z= 4√3 − i karmaşık sayısının karekökleri arasındaki uzaklık kaç br? 14
3) z= 1 − i old. göre, z−150 kaçtır? −2−75i
4) |z+4i|=2 karmaşık sayısının esas argümenti en az kaç derecedir? 240
5) z= 2 − 4i ile bu karmaşık sayının + yönde 60 derece dön. ile elde edilen karmaşık sayı arasındaki uzaklık kaç br? 2√5
z2=8cis140 karmaşık sayıları arasındaki uzaklık kaç br? 2√37
2) z= 4√3 − i karmaşık sayısının karekökleri arasındaki uzaklık kaç br? 14
3) z= 1 − i old. göre, z−150 kaçtır? −2−75i
4) |z+4i|=2 karmaşık sayısının esas argümenti en az kaç derecedir? 240
5) z= 2 − 4i ile bu karmaşık sayının + yönde 60 derece dön. ile elde edilen karmaşık sayı arasındaki uzaklık kaç br? 2√5
SORU 1
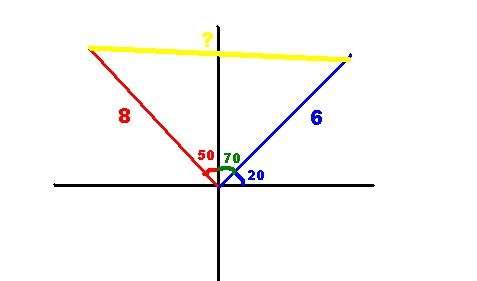
Yukarıdaki gibi koordinat düzlemine aktarıp kosinüs teoremi yaparsan bulabilirsin. Aradaki uzaklığı soruyor yani şekildeki sarı çizgiyi soruyor. Bunun içinde sarı çizgiye x dersek, x2= 82+62-2.6.8.(cos120) diye yazarız. cos120=-cos60=-1/2 olur
yerine yazarsak x2=148 olur x=2√37 bulunur
Yukarıdaki gibi koordinat düzlemine aktarıp kosinüs teoremi yaparsan bulabilirsin. Aradaki uzaklığı soruyor yani şekildeki sarı çizgiyi soruyor. Bunun içinde sarı çizgiye x dersek, x2= 82+62-2.6.8.(cos120) diye yazarız. cos120=-cos60=-1/2 olur
yerine yazarsak x2=148 olur x=2√37 bulunur
2. soruya biraz uğraştım fakat sonuca ulaşamadım. Bu tip cis'li şekilde yazamıyorsak
4√3 − i = (a+bi)2 şeklinde yazıyorduk. Buradan
a2-b2=4√3
2.a.b=-1
a2+b2=7 buluruz. Bu denklemlerden sonuca gidilmesi gerekiyor
4√3 − i = (a+bi)2 şeklinde yazıyorduk. Buradan
a2-b2=4√3
2.a.b=-1
a2+b2=7 buluruz. Bu denklemlerden sonuca gidilmesi gerekiyor
SORU 3
z=1-i'yi cis'li şekilde yazalım. lzl=√2 olur. cos=√2/2 ve sin= -√2/2 bulunur. Yani 4. bölgeden 45 derecelik açıyla alıcağız cis'i. Buda cis(360-45)=cis315 bulunur. Uzunluğumuzla düzenlersek w=√2.cis(315) bulunur. -150 üssünü alacağız. Önce uzunluğu alalım √2-150 = 2-75 olur. Şimdi cis'imize bakalım. Bunun içinde açımızı üs ile çarpmamız gerekiyor. Yani cis (-150 . 315) = cis (-90) bulunur. Burada çarpma yapıp 360'a bölerek kalanı bulabilirsin ben öyle yaptım -90 yazdım. Ama 315'i 45 olarak görüp -150 ile çarpabilirsin. Yine aynı şey çıkacaktır. cis(-90) açımız - olamayacağından 360 ekleriz ve cis270 elde ederiz. Şimdi karmaşık sayımızı düzenli bir şekilde yazalım. w= 2-75 . cis270 'dir. cis 270 de (cos270+sin270) olduğundan cis270=(0-i) bulunur. Şimdi son haline getirelim 2-75. -i buradan cevap -2-75i olur.
Biraz uzun oldu ayrıntıya fazla girdim sanırım kusura bakma umarım anlamışsındır anlamadığın bir yer olursa sor lütfen
z=1-i'yi cis'li şekilde yazalım. lzl=√2 olur. cos=√2/2 ve sin= -√2/2 bulunur. Yani 4. bölgeden 45 derecelik açıyla alıcağız cis'i. Buda cis(360-45)=cis315 bulunur. Uzunluğumuzla düzenlersek w=√2.cis(315) bulunur. -150 üssünü alacağız. Önce uzunluğu alalım √2-150 = 2-75 olur. Şimdi cis'imize bakalım. Bunun içinde açımızı üs ile çarpmamız gerekiyor. Yani cis (-150 . 315) = cis (-90) bulunur. Burada çarpma yapıp 360'a bölerek kalanı bulabilirsin ben öyle yaptım -90 yazdım. Ama 315'i 45 olarak görüp -150 ile çarpabilirsin. Yine aynı şey çıkacaktır. cis(-90) açımız - olamayacağından 360 ekleriz ve cis270 elde ederiz. Şimdi karmaşık sayımızı düzenli bir şekilde yazalım. w= 2-75 . cis270 'dir. cis 270 de (cos270+sin270) olduğundan cis270=(0-i) bulunur. Şimdi son haline getirelim 2-75. -i buradan cevap -2-75i olur.
Biraz uzun oldu ayrıntıya fazla girdim sanırım kusura bakma umarım anlamışsındır anlamadığın bir yer olursa sor lütfen
korkmazserkan 15:26 04 Eyl 2014 #5 z= 1 − i old. göre, z-150 kaçtır?
[1/(1-i)]150=[(1-i)/(1-i)²]150
=(-2i)75/(-2i)150
=(-2i)-75
=-2-75.i
.............................................
(1-i)²=-2i
[1/(1-i)]150=[(1-i)/(1-i)²]150
=(-2i)75/(-2i)150
=(-2i)-75
=-2-75.i
.............................................
(1-i)²=-2i
Nasılyaniya 19:10 05 Eyl 2014 #6
Çok sağ olun, 2 yolu da anladım 
Son sorulara da yardımcı olabilecek varsa sevinirim
Son sorulara da yardımcı olabilecek varsa sevinirim
korkmazserkan 19:15 05 Eyl 2014 #7
çizim istiyor şu an üşengeçliğim üstümde 
Nasılyaniya 19:19 05 Eyl 2014 #8
Acelem yok, ne zaman istersen