fonksiyon

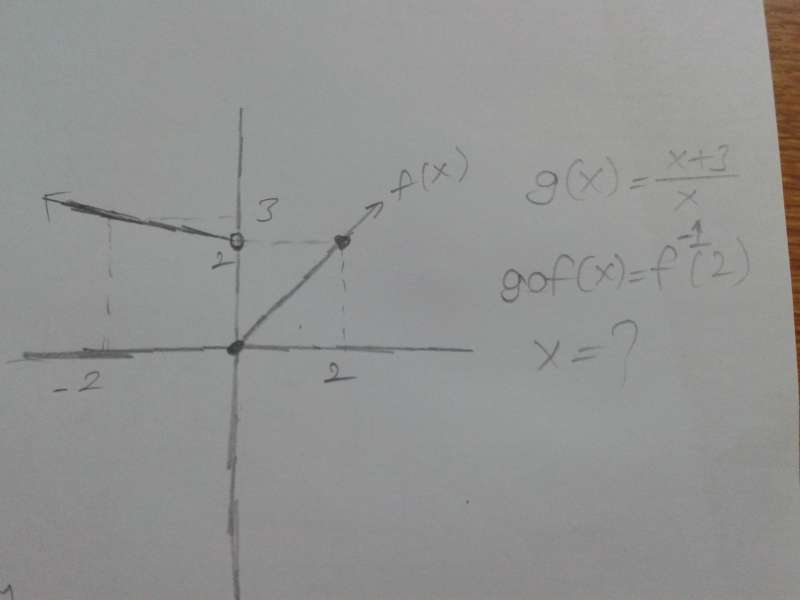
fotoğraftaki sorunun çözümünü yaptım fakat f(x) fonksiyonunu parçalı fonksiyon biçiminde yazdığımızda sonuca ulaşamıyoruz, yardımcı olabilecek arkadaşlara şimdiden çok teşekkürler

Merhaba..f(x)'in tersi için f-1(x) yazacağım..
Önce f(x)'i parçalı fonksiyon hâlinde yazmaya çalışalım..
0'ın kırılma noktası olduğu açık,öyleyse parçalı fonksiyonda sınırlar 0'a göre düzenlenecek..
Şimdi x≥0 için f(x)=x olduğu görülüyor..
x<0 içinse doğrusal denklem sisteminden f(x)=(4-x)/2 bulunur..(x=0 için y=2 ve x=-2 için y=3 bunu kullanarak doğru denklemi çizdik)
Şimdi bunlarla fonksiyonu oluşturalım..

             x≥0     x

f(x)={                           }

             x<0     (4-x)/2

Şimdi bir de f-1(x)'i bulalım..
Parçalı fonksiyonun tersi bulunurken,önce parçaların sınırları bulunur..Fonksiyonun şu anki hâlinde verilen x sınırlarını yanda bulunan kurala uyguladığımızda f(x) (yâni y değeri) kaçtan büyük oluyorsa veya kaçtan küçük oluyorsa bunu fonksiyonun tersinde x'in sınırları olarak belirlemeliyiz..
Dikkat edilmesi gereken diğer bir şey ise grafiğin yanlış çizilmiş olması..x'in 0'dan büyük olduğu yerlerde f(x)'in grafiği sonsuza kadar gitmez,giderse tersi olmaz..

Buna göre fonksiyonun tersi

                x≤2     x  

f-1(x)={                      }

                x>2     4-2x

g(x)=(x+3)/x ve g(f(x))=f-1(2)
x=?
burada önce f-1(2)'yi bulalım..Bulduğumuz parçalı fonksiyona göre f-1(2)=2
Şimdi bunu yerine yazalım..
g(f(x))=2 (g'de x gördüğümüz yerlere f(x) yazarsak sonuç 2 olacakmış)

g(x)=(f(x)+3)/(f(x)=2

2.f(x)=f(x)+3
f(x)=3
f(x)'in hazırladığımız parçalı fonksiyonuna bakarsak x<0 için f(-2)=(4-(-2))/2=3
Demek ki x=-2'ymiş..

Umarım hata yapmamışımdır..