1
[(x²+3x-4)/x]-[(6x)/(x²+3x-4)]=5 denkleminin reel köklerinin toplamı kaçtır? (-6)
2
3
4
log2 tabanında (2x-1)=m eşitliğini gerçekleyen x bir çift tam sayı, m bir doğal sayıdır. Kaç farklı m sayısı yazılır? (5)
5
z1=3cis170
z2=3cis50 ise |z1+z2|=? (3)
6
o
d d
t t t
ü ü ü ü (boşlukları yutmuş ama paskal üçgeni gibi olmalıydı, anladınız sizler.)
yukarıdaki harf tepesinden (o-dan) başlayarak aşağı ve sağa-sola hareket ederek ODTÜ yazılacaktır. Kaç farklı rota belirlenebilir? (8)
7
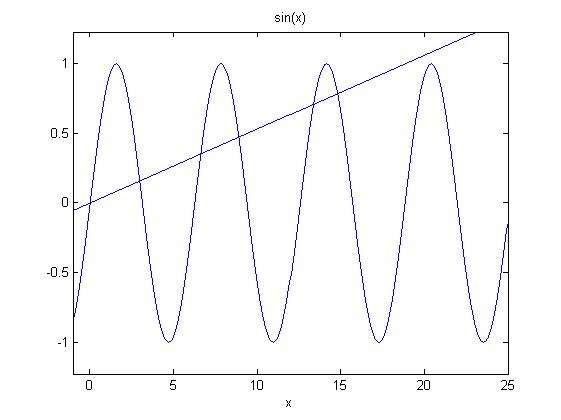
sinx=x/6pi denkleminin (0,∞) aralığında kaç kökü vadır? (5)
8
881 882
883 884 matrisinin determinantı kaçtır? (-2) (+2 olmaz mıydı?)
[(x²+3x-4)/x]-[(6x)/(x²+3x-4)]=5 denkleminin reel köklerinin toplamı kaçtır? (-6)
2
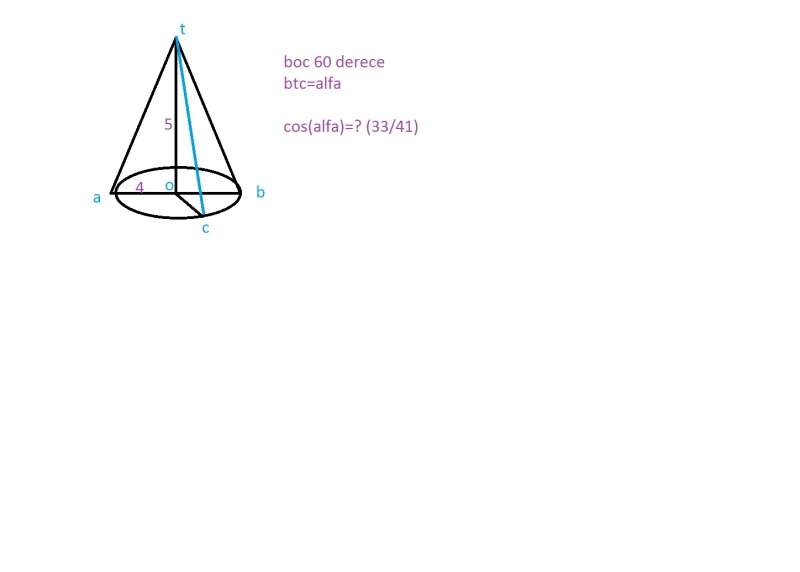
3
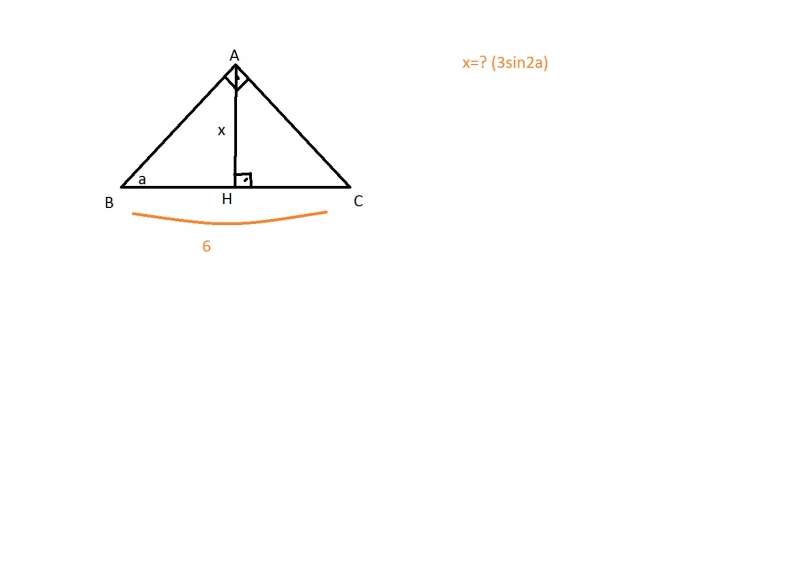
4
log2 tabanında (2x-1)=m eşitliğini gerçekleyen x bir çift tam sayı, m bir doğal sayıdır. Kaç farklı m sayısı yazılır? (5)
5
z1=3cis170
z2=3cis50 ise |z1+z2|=? (3)
6
o
d d
t t t
ü ü ü ü (boşlukları yutmuş ama paskal üçgeni gibi olmalıydı, anladınız sizler.)
yukarıdaki harf tepesinden (o-dan) başlayarak aşağı ve sağa-sola hareket ederek ODTÜ yazılacaktır. Kaç farklı rota belirlenebilir? (8)
7
sinx=x/6pi denkleminin (0,∞) aralığında kaç kökü vadır? (5)
8
881 882
883 884 matrisinin determinantı kaçtır? (-2) (+2 olmaz mıydı?)
mathematics21 00:30 09 May 2013 #2 1) Payda eşitleyip düzenleyelim:
(x²+3x-4)2-5x(x²+3x-4)-6x²=0
çarpanlarına ayıralım: (Daha iyi görmek için x²+3x-4 = y diyebilirsiniz)
(x²+3x-4-6x)(x²+3x-4+x)=0
(x²-3x-4)(x²+4x-4)=0
buradaki iki çarpandan da gelen kökler reel olacaktır. x²-3x-4=0 ifadesinden gelen kökler toplamı 3, x²+4x-4=0 ifadesinden gelen kökler toplamı -4 tür. Yani cevap -1 olmalı. Cevabınızı kontrol edin lütfen.
(x²+3x-4)2-5x(x²+3x-4)-6x²=0
çarpanlarına ayıralım: (Daha iyi görmek için x²+3x-4 = y diyebilirsiniz)
(x²+3x-4-6x)(x²+3x-4+x)=0
(x²-3x-4)(x²+4x-4)=0
buradaki iki çarpandan da gelen kökler reel olacaktır. x²-3x-4=0 ifadesinden gelen kökler toplamı 3, x²+4x-4=0 ifadesinden gelen kökler toplamı -4 tür. Yani cevap -1 olmalı. Cevabınızı kontrol edin lütfen.
-6 demiş hocam, hatalıdır o halde.
mathematics21 00:38 09 May 2013 #5 2
4) 2x-1=2m olur yalnız burda 2x-1 her türlü tek bir sayıdır oysa ki 2m in 0 haricindeki bütün doğal sayı üsleri çifttir böyle olursa x tam sayı olmaz ve çift olup olmadığını anlayamayız
4.soruda tuhaflık var x çift tamsayı ise 2x-1=tek sayı o zaman 2^m her zaman çift olduğu için m=0 için tek değer olur
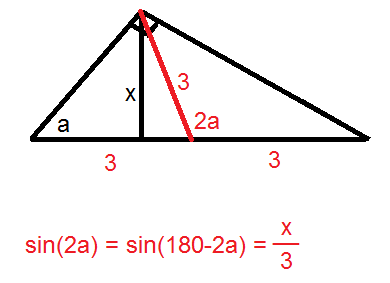
mathematics21 00:45 09 May 2013 #8 3)
mathematics21 01:17 09 May 2013 #10 8) 881 yerine a yazınca determinantı a(a+3)-(a+1)(a+2) = -2 olarak bulursunuz.
7) Dün buna benzer bir soru sorulmuştu. Tasvip etmediğim soru türlerinden ama bugün biraz farklı bir cevap yazayım:
y=x/6pi doğrusunun eğimi 1/6pi dir. Bu doğruya d doğrusu diyelim.
Biz y=sinx fonsksiyonun yerel maksimum noktlarını düşünelim:
x=pi/2 için sinx = 1 dir. (pi/2, 1) noktasından ve orijinden geçen doğruyu düşünelim. Bu doğrunun eğimi 2/pi dir. Bu doğruya a1 doğrusu diyelim.
1/6pi < 2/pi olduğu için birinci bölgede a1 doğrusu d doğrusunun üstündedir.
Amacımız d doğrusunu arasına alacak iki doğru bulmak. Tabii ki bu iki doğrunun her biri sinx fonksiyonun yerel maksimum noktalaarından birinden ve orijinden geçmeli.
x=5pi/2 için sinx = 1 dir. (5pi/2, 1) noktasından ve orijinden geçen doğruyu düşünelim. Bu doğrunun eğimi 2/5pi dir. Bu doğruya a2 doğrusu diyelim.
1/6pi < 2/5pi olduğu için birinci bölgede a2 doğrusu d doğrusunun üstündedir.
Benzer şekilde devam edersek sırasıyla 3. ve 4. tepe noktalarını orijinle birleştiren doğrular d doğrusunu aralarına alacaktır. Her iki tepe noktası arasında d doğrusu y=sinx eğrisini iki defa keseceğinden toplamda 5 kesişim noktası, yani 5 pozitif kök, olur.
7) Dün buna benzer bir soru sorulmuştu. Tasvip etmediğim soru türlerinden ama bugün biraz farklı bir cevap yazayım:
y=x/6pi doğrusunun eğimi 1/6pi dir. Bu doğruya d doğrusu diyelim.
Biz y=sinx fonsksiyonun yerel maksimum noktlarını düşünelim:
x=pi/2 için sinx = 1 dir. (pi/2, 1) noktasından ve orijinden geçen doğruyu düşünelim. Bu doğrunun eğimi 2/pi dir. Bu doğruya a1 doğrusu diyelim.
1/6pi < 2/pi olduğu için birinci bölgede a1 doğrusu d doğrusunun üstündedir.
Amacımız d doğrusunu arasına alacak iki doğru bulmak. Tabii ki bu iki doğrunun her biri sinx fonksiyonun yerel maksimum noktalaarından birinden ve orijinden geçmeli.
x=5pi/2 için sinx = 1 dir. (5pi/2, 1) noktasından ve orijinden geçen doğruyu düşünelim. Bu doğrunun eğimi 2/5pi dir. Bu doğruya a2 doğrusu diyelim.
1/6pi < 2/5pi olduğu için birinci bölgede a2 doğrusu d doğrusunun üstündedir.
Benzer şekilde devam edersek sırasıyla 3. ve 4. tepe noktalarını orijinle birleştiren doğrular d doğrusunu aralarına alacaktır. Her iki tepe noktası arasında d doğrusu y=sinx eğrisini iki defa keseceğinden toplamda 5 kesişim noktası, yani 5 pozitif kök, olur.