1
Bir hileli madeni parada tura gelme olasılığı 1/3'tür. Bu para 3 kez havaya atıldığında 2 yazı 1 tura gelme olasılığı kaçtır? (4/9)
2
Bir çift zar atılıyor. Zarlardan birinin 3 geldiği bilindiğine göre üst yüze gelen sayılar toplamının 8 olma olasılığı kaçtır? (2/11)
3
2 öğretmen, 3 doktor, 4 öğrenci, 2 hemşire arasında 4 kişi seçielecek olup bu 4 kişinin farklı mesleklerden olma olasılığı kaçtır? (8/55)
4
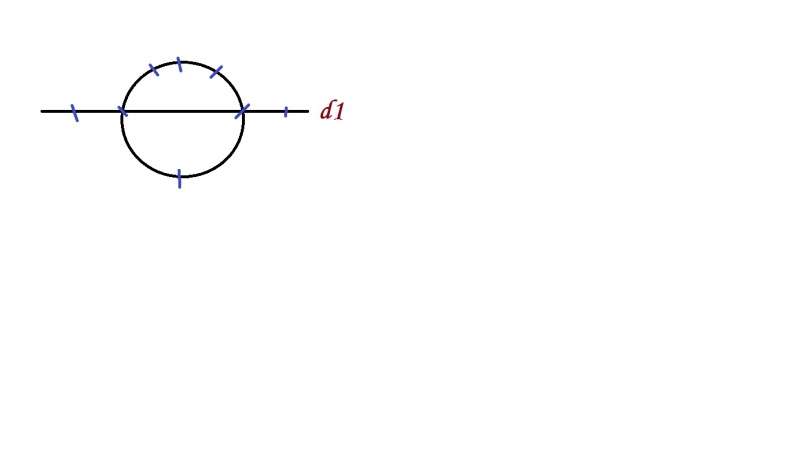
8 noktadan seçilen 3 noktanın sadece birinin d1 üzerinde olma olasılığı kaçtır? (3/7)