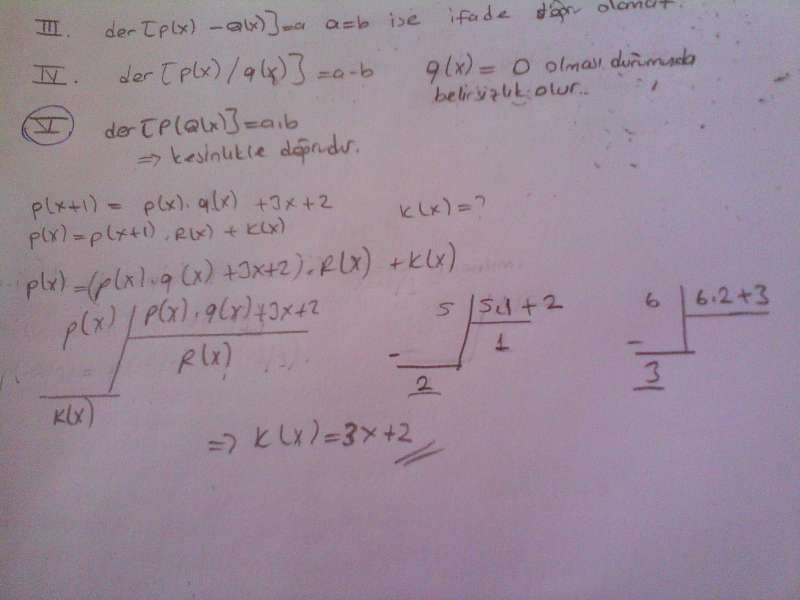polino-denklem

1) der(P(x))=a der(Q(x))=b ve a≥b
olmak üzere

I.der[P(x)+derQ(x)]=a
II.der[P(x).Q(x)]=a+b
III.der[P(x)-Q(x)]=a
IV.der[P(x)/Q(x)]=a-b
V.der[P(Q(x))]=a.b ifadelerinden kaç tanesi kesinlikle doğrudur? (Cevap 2)


2) P(x+1)=P(x).Q(x)+3x+2 P(x)=P(x+1).R(x)+K(x) ise K(x) nedir? (Cevap: -3x-2)

3) (x+2)⁵.(x²+3x-2) polinomunun (x+2)⁶ polinomuna bölümünden kalan nedir? (Cevap -4.(x+2)⁵ burda cevabın -4 olması gerekmez mi???))

4) x²-(2a+b-3)x+a²-5a=0 denkleminin simetrik ve sıfırdan farklı iki reel kökü olduğuna göre b'nin alabileceği tamsayı değerlerinin toplamı nedir? (-18)

5)İki basamaklı en büyük asal sayı x, en küçük asal sayıy dir. x-k.y=A ve A asal sayı olmak üzere k kaç farklı değer alır? (k∈Z⁺) (Cevap 24)


6) Bir doğal sayının karesi, altı basamaklı (abcdef) sayısıdır. e rakamı tek olduğuna göre , e+f nin alabileceği en büyük değer nedir? (17)

7) Z/5 te √11+3^-2 toplamının eşiti nedir? (ben iki farklı cevap buluyorum birisi 0 diğeri 3 cevap 3 müş köklü sayıyı nasıl çıkaracaz dışarıya iki farklı şekilde çıkıyor)

Sorular Mükemmel !
C.3

(x+2)⁵=t olsun.Bizden istenen t.(x²+3x-2) ifadesinin t.(x+2)^5 ifadesi ile bölümünden kalan.

Şimdi kalan sorularında sadeleştirme yapamayız bu nedenle hemen (x+2)^5 kısımları sadeleşir diyemez.

(x+2)^6 = t.(x+2) olduğundan x=-2 yazalım istenen ifadede bizden istenen

t.(x²+3x-2) => t.(4-6-2) => -4t olur ki sadeleştirme yapamadığımız için -4.(x+2)^5 olur diye düşünüyorum.

Hatta bununla ilgili benzer bi soru sorulmuştu ama faktöriyeldendi 6!+7! / 5!+... bişeylerdi işte kalanı soruyordu hemen sadeleştirme yapamayız bu tıpkı 4.3/2 ifadesindeki kalanı sorarken sadeleştirme yaparsak kalanı 6 bulmak gibi bi şeyolur.

sadeleşme yapamayacağımızı anladım ama çözümün sırrı acaba modüler aritmetikle ilgili mi onu merak ettim sonuçta polinom bölmesi yapsam kalan negatif gelmez heralde

(x+2)^5 li bir terimi (x+2)^6 lı bir ifadeye bölüyoruz kalan negatif gelebilir bence.
Mesela 4ü 6'ya -2 kalanı geliyor bence böyle bir ilişki olabilir ki çözüm böyle olmalı bence.

Bide , polinom bölmesi yapsana bi böyle geliyor herhalde yine. .Bence böyle olmalı.

4
bir bunu çözebildim
kökler simetrik ise toplamları 0, y eksenine göre simetrik ve reel
2a+b=3

kökler çarpımı ise negatif olur.
a²-5a<0, a=0 ve a=5 için incelenirse
a=0 için b=3
a=5 için b=-7 olur

tablo (-7,3) aralığında

Resimle gondereyim 1. Soruyu

Resimde yanlis yazmisim +2 ile yazan yer ve +3 ile yazan yer -2 ve -3 olacakti
Sonucta negatif olur.

Ayrıca sonuç -4 olsaydı şu da sağlamalıydı.

(x+2)⁵.(x²+3x-2) = (x+2)^6.Q(x)+K
x=-2 için 0 = -4 gibi bir şey olur ki bu da sağlamaz zaten.

-4.(x+2)⁵ => Kalan bu halde olunac 0=0 olur.

5) x=97 ve y=2 olduğundan 97-2k=A
burada A sayısıda asal ve tek sayı olduğundan 3 ten 97 ye kadar toplam 24 asal var

6) cevap 17 verilmiş ama e=9 f=8 almanız gerek bu cevap için fakat hiçbir doğal sayının karesi abcd98 şeklinde olmaz (neden?) ipucu mod4 düşünün

7) yaptığınız doğru gibi duruyor cevap 0 yada 3 olmalı

C.3
(x+2)⁵.(x²+3x-2) polinomunun (x+2)6 polinomuna bölümünden kalan nedir?
Savaş haklı. Çözüm şu şekilde:
(x+2)⁵.(x²+3x-2)=(x+2)⁶.B(x)+K(x) olsun.
Eşitliğin sol tarafı 7. dereceden olduğundan; d(B(x))=1 olmalı. a,b ∈ R olmak üzere B(x)=ax+b gibidir.
Eşitliğin sol tarafından 7. dereceden bir tek x⁷ gelir. Sağ taraftan ise; ax⁷ gelir. Dolayısıyla a=1 'dir. B(x)=x+b olur.
Eşitliğin sol tarafından 6. dereceden 13x⁶ gelir. Sağ taraftan ise; (m+12).x. (Zaten bölen 6. dereceden olduğundan; K(x)'in içinde 6. dereceden bir ifade olamaz.) O halde m=1 olur. B(x)=x+1 olur. Yani;
(x+2)⁵.(x²+3x-2)=(x+2)⁶.(x+1)+K(x) olur.
(x+2)⁵.(x²+3x-2)-(x+2)⁶.(x+1)=K(x) olur.
(x+2)⁵.(x²+3x-2-(x+2).(x+1))=K(x)
(x+2)⁵.(-4)=K(x) olur.