karışık matematik sorularım

1) 1 den 12 ye kadar numaralandırılmış 12 kartın bulunduğu bir torbadan çekilen kart torbaya geri atılmamak şartıyla ard arda iki kart rasgele çekiliyor. Birinci karttaki sayının ikinci karttaki sayıdan küçük bir çift sayı olduğu bilindiğine göre ikinci karttaki sayının 3 ün katı olma olasılığı kaçtır?
a)3/5 b)7/10 c)2/5 d)1/3 e)1/2

2)



sağlayan x tam sayıları toplamı kaçtır?
a)-1 b)1 c)2 d)3 e)8

3)A={0,1,2,3,4,5,6} kümesinin elemanları kullanılarak 246 dan büyük rakamları farklı üç basamaklı kaç değişik doğal sayı yazılabilir?
a)90 b)100 c)120 d)130 e)150
4)


5)

C-5

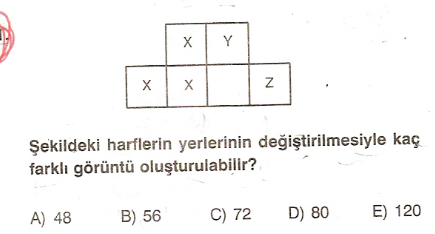
3 tane x, 1 tane y, 1 tane z, 1 tane de boş kutu kaç farklı şekilde yerleştirilebilir.

Eğer hepsi birbirinden farklı kutular olsaydı, 6! farklı şekilde olurdu. Ancak 3 tane x olduğundan tekrarlı permütasyon, 6!/3!=120 farklı diziliş olur.

C-3

__ __ __

Sayısının ilk basamağı 2 olsun.

2 __ __

İkinci basamak 4'ten büyük olmalı ki istenen şart sağlansın, İkinci basamağa C(2,1)=2 farklı seçim yapılır.
Son basamağa geri kalan sayılardan C(5,1)=5 farklı seçim yapılabilir.
Bu şekilde yazılabilen sayılar 2.5=10 tanedir.

Eğer ilk basamak 2'den büyük olursa, C(4,1)=4 farklı seçim yapılır.
İkinci basamağa C(6,1)=6
Üçüncü basamağa C(5,1)=5 farklı seçim yapılır.
Bu şekilde yazılabilen sayılar, 6.5.4=120 tanedir.

Toplamda, 120+10=130 tane sayı yazılır.

C-3


A={0,1,2,3,4,5,6} kümesinin elemanları kullanılarak 246 dan büyük rakamları farklı üç basamaklı kaç değişik doğal sayı yazılabilir?

2 ile de başlayabilir 2 _ _ ikinci kutucuğa 5,6 , diğer kutucuğa 5 tane yazılır. 2.5 = 10 tane yazılır.


3,4,5,6 ile başlayanlara bakarsak .

3 ile başlayan için = ikinci kutucuğa 6 tane diğerine 5 tane 6.5 =30 tane yazılabilir.4 tane böyle var 30.4 = 120 tane yazılabilir.

toplam dada 120+10 =130 olur

C-1

1. karttaki sayıyı farzederek kac durum oldugunu hesaplarız.
eger 1. karttaki sayı
- 2 ise 2. karttaki sayının alacağı 10 değer var. 10 ihtimal (3ün katı olma ihtimali de 3,6,9,12 den 4 tanedir.)
- 4 için 8 değer var (6,9,12 değerleri sağlar, 3 tanedir.)
- 6 için 6 değer var (9,12 sağlar, 2 tane)
- 8 için 4 değer var (9,12 sağlar, 2tane)
- 10 için 2 değer var (12 sağlar, 1 tane)
- 12 için 2. karttaki sayının alacağı herhangibir deger yok.

yani toplam durum: 10+8+6+4+2=30 dur.
istenen durum: 4+3+2+2+1=12 dir. 12/30 dan 2/5 çıkar.

C-1

Verilen şarta göre, büyük kart 12 iken, küçük kart 10,8,6,4,2 yani 5 farklı değer alıyor.
Büyük kart 11 iken yine aynı, 10,8,6,4,2 yani 5 farklı değer alıyor.
Büyük kart 10 iken, 8,6,4,2 yani 4 farklı değer alıyor.
Büyük K=9 için 4 farklı değer,
B.K= 8 için 3 farklı değer,
B.K=7 için 3 farklı değer,
B.K=6 için 2 farklı değer,
B.K=5 için 2 farklı değer,
B.K=4 için 1 farklı değer,
BK=3 için 1 farklı değer alır.

Toplamda, 2(5+4+3+2+1)=30 farklı çekim yapılabiliyor.

Büyük kartın 12k olduğu değerler kaç tane bakalım,
12 için 5
9 için 4
6 için 2
3 için 1
+_____
12 tane

30 değerden 12 tane ise, 12/30=2/5 ihtimal vardır.

C-2

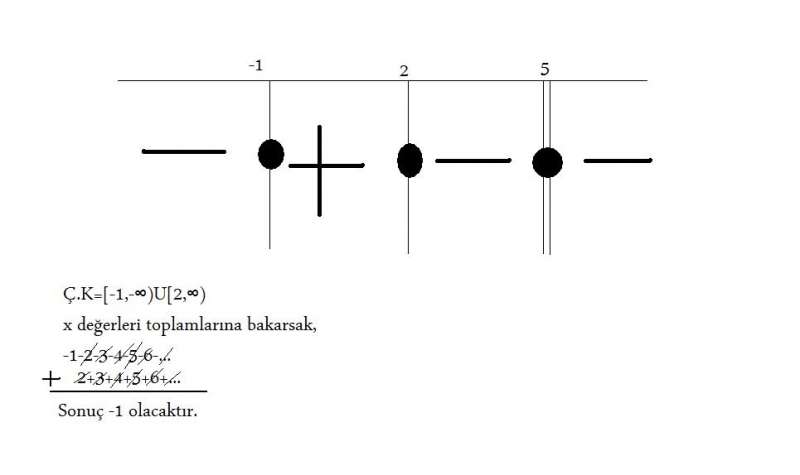
Köklerini bulalım,

x-2=0
x=2

5-x=0
x=5 (4. dereceden kuvveti olduğu için çift katlı kök)

x+1=0
x=-1

x katsayıları çarpımı negatif olduğundan tablo negatif ile başlar.

4)
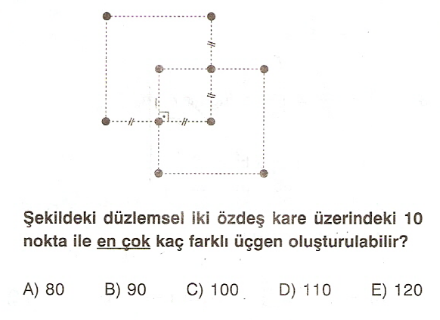
10 noktanın hiçbiri düzlemsel olmasaydı
C(10,3)=120 üçgen olurdu.
Şimdi, iki karenin ortak köşegeni olan kb-gd doğrultusundaki 4 noktalı köşegen (I)
haricindeki ,
üzerinde 3 nokta işaretlenmiş toplam köşe veya kenarların sayısı 6 dır.

(I) nolu durumdaki köşegenin üzerindeki 4 noktadan 3 nokta C(4,3)=4 farklı şekilde seçileceğinden ve bu noktalarla üçgen oluşmayacağından
6+4=10 tane seçim için üçgen oluşmaz.
O zaman 120-10=110 tane üçgen oluşturulabilir.

anladım şimdi ben çift katlı kök olduğundan - işaret + ya dönüşür diye düşünmüştüm demek ki çok yanlış düşünmüşüm kuvvetin bir önemi yok yani sadece parentez içinde en büyük dereceli terimin katsayısına bakılacak

bi şey daha sorucam o zaman -1 değerini almamamız gerekmiyor mu paydayı 0 yapıyor almayınca da cevap 0 çıkıyor. 0 şıklarda yok?