karışık matematik sorularım

Z= cos 110(cos 370 +isin 370) ifadesinin esas argümenti nedir?
a)10 b)20 c)70 d)110 e)190
2)
Aylık 56 makine üretme kapasiteli bir fabrika ürettiği her makineyi 2000tl ye satıyor.Fabrika, makinelerin satış fiyatına her ay düzenli olarak 400tl zam yaptığında makine satışlarında her ay 4 tane azalma oluyor. Bir makinenin maliyeti 1200tl old. göre maksimum karın elde edildiği ayda kaç tane makine üretilmiştir?
a)52 b)48 c)36 d)32 e)24
3)
a+b =∏/6 tan b=1/5 ise cot (6a+5b)=?
a)-5 b)-5/3 c)-3/5 d)3/5 e)5
4)39!+38!= 4^x.5^y.a olduğuna göre x+y en çok kaçtır?
a) 28 b)26 c)24 d)20 e)15
5)



a)1/n-1 b)1/n c)1+1/n d)n/n+1 e)1/n+1

3) a+b=30 verilmiş. (6a+5b) yi 5(a+b)+a yazabiliriz.a+b=30 sorulan açı cot(150+a) olmuş oldu bunuda cot(90+60+a) şeklinde yazarız.

90 dercede isim değişirdi.tan oldu tan(60+a) bulmamız lazım fakat 90+60+a açısı 2. bölgededir (a açısı dar ve 30 dan küçük çünkü a+b zaten 30) 2. bölgede sadece sin artıdır diğerleri( -) cot da - ifadenin başına - yazarız -tan(60+a) oldu.




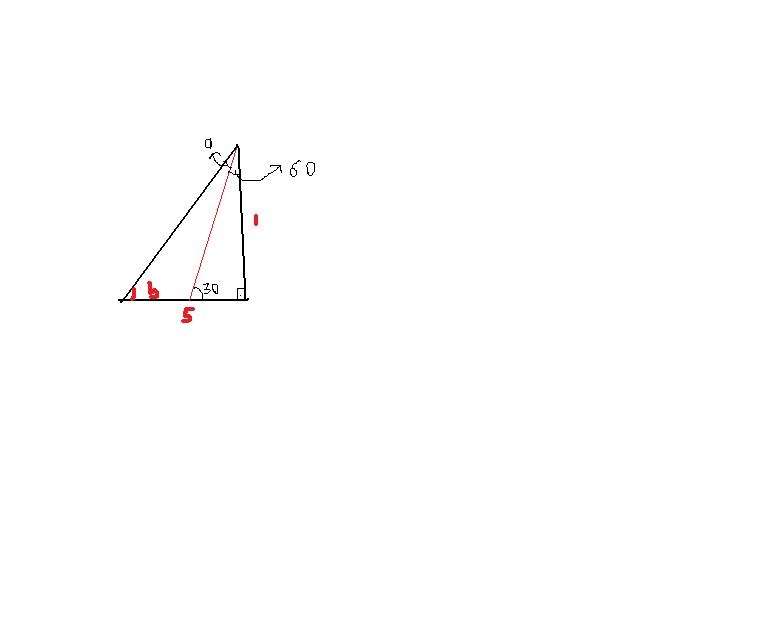
dik üçgende tepedeki açı 60+a açısı oldu bizde zaten o açıyı arıyorduk bu açının tanjantı 5 tir.-tan(60+a)= -5 buldum hata yapmadysak

4)39!+38!=4^x.5^y a olduğuna göre x+y en çok kaçtır?

38! parantezine alırsak 38!.(1+39)=(38!.40)=2^2x.5^y.a (2 ve 5 asal çarpanlrının 38! ve 40 ın içinde kaç tane olduğuna bakmalıyız 40 = 8.5 olduğundan 2³.5 3 tane 2 ve bir tane 5 var 38! de ise;

1.2.3.4.5.........35.36.37.38 =38! (tek tek 2 çarpanını ve 5 çarpanını aramak zor olacağından 38 `i 2 ye ve 5 e bölünmeyene kadar bölerek sonrada bölümleri toplayarak içine kaç tane 2 ve 5 çarpanları olduğunu bulabiliriz)

38 / 2= 19 19/2=9 9/2=4 4/2=2 2/2=1 (kalan olup olmaması önemli değil bölümler önemli ) (bölümleri toplarsak 35 yapar 3 tanede 40 dan gelen 2 çarpanımız vardı 38 oldu.(38 tane 2 çarpanı varmış)

5 çarpanını bulmak içinde aynı şekilde 38 i sürekli 5 bölüp bölümleri topladığımızda 8 çıkar bir tane de 40 dan gelen var 9 tanede 5 çarpanı oldu.

2^2x 2x=38 ise x=19 y=9 x+y=28 (birde a çarpanı vardı buda 2 ve 5 hariç diğer çarpanlar)bizden 2 ve 5 çarpanı kaç tane o sorulmuş.

2. sorunun cevabı 32 mi doğruysa anlatayım değilse kafanı karıştırmak istemem.

Ben de buldum sonucu , 32 çıkıyor.(Türevle yaptım ama , umarım doğru bir mantıkla gitmişimdir x.aya f(x) vs.dedim) herneyse , eğer siz yapcaksanız buyrun yapın , buraya kendi çözümümü yazıp size saygısızlık etmek istemem.Cevabınız doğru

Aynen bende türevden yaptım ama biraz uzuyor çözümü size bırakmak işime gelir buyrun siz yapın
yalnız bişey merak ettim iş bilginizde 9.sınıf yazıyor ama türev biliyosunuz şimdiden nasıl

türevin tamamını sorsan bilmem , ama geçen yıllarda yaz tatillerimde bilgisayar dilleri öğrenmeye merak salmıştım , o aralar öğrenmek zorunda kalmıştım biraz tamam çözüyorum.

Aylık 56 makine üretme kapasiteli bir fabrika ürettiği her makineyi 2000tl ye satıyor.Fabrika, makinelerin satış fiyatına her ay düzenli olarak 400tl zam yaptığında makine satışlarında her ay 4 tane azalma oluyor. Bir makinenin maliyeti 1200tl old. göre maksimum karın elde edildiği ayda kaç tane makine üretilmiştir?

1.Ay kar => (56-4).(2000+400) - (56.4).(1200)
2.Ay kar => (56-8).(2000+800) - (56.8). (1200
şeklinde olacaktır...

Satışların maximum olduğu ayımız x. ayımız olsun.

1.Ay kar => (56-4).(2000+400)- (56.4).(1200)
2.Ay kar => (56-8).(2000+800)- (56.8). (1200
X.Ay kar => (56-4x).(2000+400x)-(56.4x).(1200) şeklinde olur.


h(x) , x.aydaki karımızı gösteren bir fonksiyon olsun.
Örneğin h(1) , 1.aydaki karımızı gösterir.

h(x) = (56-4x).(2000+400x)-(56.4x).(1200) şeklinde olur.

h(x) = (56-4x).((2000+400x)-1.(1200)) olur.(Ortak çarpan parantezine aldık.)

h(x) = (56-4x).((800+400x)) olur.Çarpımın türevi kolaylık sağlıyacaktır.

h'(x) = 4.(800+400x) + (56-4x).400=0 olur.

Buradan x=6 bulunur.

h(x) = (56-4x).((800+400x)) ' idi h(6) aranıyor.

koyu ile belirtilen satılan makine sayımızı belirtiyordu.

o halde , x=6 için , koyu kısım 56-24 => 32 bulunur.

türevsiz de yapabilirsiniz
yapılan zam sayısı n olsun
o zaman birim başına kar (8+4n) olur (100 leri sildim)
sayılan makine sayısı da (56-4n)
bizden (8+4n).(56-4n) in max olmasını istiyor , dikkat edilirse toplamları 64 (n e bağlı değil) yani en büyük değerini sayılar 32 olduğunda alır. kontrol edilmesi gereken soruda gizli olarak verilen tamsayı koşullarının 32 için sağlanıp sağlamadığı, o da görüldüğü gibi sağlanıyor. mesela 33 çıksaydı 33 alamazdık onun yerine sağ ve sol yanındaki tamsayıda uygun sayıları yani 32 ve 36 yı dener hangisi büyük değer veriyorsa onu alırdık.

sadece 1. soru kalmış galiba
cos110 negatif bi reel sayı olduğundan argumenti 180 olur
diğerinin argumenti de 10 verilmiş zaten
sonuç 190 olur