1)
0<x<360 olmak üzere sin 3x=1/2 denkleminin kaç kökü vardır?
a)2 b)3 c)4 d)5 e)6
2)
2x²-8x+k-2=0 denkleminin reel kökleri x1 ve x2 dir. x1.x2 nin alabileceği max değer =?
a)5 b)4 c)3 d)2 e)1
3)


5)

0<x<360 olmak üzere sin 3x=1/2 denkleminin kaç kökü vardır?
a)2 b)3 c)4 d)5 e)6
2)
2x²-8x+k-2=0 denkleminin reel kökleri x1 ve x2 dir. x1.x2 nin alabileceği max değer =?
a)5 b)4 c)3 d)2 e)1
3)

5)

C-4)
Sayı dizisi:
6,6,6,6,6,6,7,7,7,7,7,7,7,8,8,8,8,8,8,9,9,9,9,9,9,9,9 = 27 tane. Ortanca değer 13 sağ 13 sol olarak düşünülürse geriye kalan baştan 14. değer 8 dir.
İlk 13 terim alt grup. Bunun ortanca değeri : 6,6,6,6,6,6,7,7,7,7,7,7,7 ; 7 dir.
Son 13 terim üst grup. Bunun ortanca değeri : 8,8,8,8,8,9,9,9,9,9,9,9,9 : 9 dur.
Cevap: 8,7,9 (B Seçeneği)
Sayı dizisi:
6,6,6,6,6,6,7,7,7,7,7,7,7,8,8,8,8,8,8,9,9,9,9,9,9,9,9 = 27 tane. Ortanca değer 13 sağ 13 sol olarak düşünülürse geriye kalan baştan 14. değer 8 dir.
İlk 13 terim alt grup. Bunun ortanca değeri : 6,6,6,6,6,6,7,7,7,7,7,7,7 ; 7 dir.
Son 13 terim üst grup. Bunun ortanca değeri : 8,8,8,8,8,9,9,9,9,9,9,9,9 : 9 dur.
Cevap: 8,7,9 (B Seçeneği)
1) de işlemi tam toparlayamadım ama 2 kök varmış gibime geliyor şu an acelem var gelince tekrar bakmaya çalışırım
sin3x=1/2
sin 1/2 olması için ∏/6 ve 5∏/6 olması lazım
3x=∏/6+2∏n ve 5∏/6+2∏n
x=∏/18+2∏/3n ve 5∏/18+2∏/3n bu şartları sağlar
sin 1/2 olması için ∏/6 ve 5∏/6 olması lazım
3x=∏/6+2∏n ve 5∏/6+2∏n
x=∏/18+2∏/3n ve 5∏/18+2∏/3n bu şartları sağlar
1.
sin x her periyotta 2 kez 1/2 değerini alacaktır. sin3x verildiğinden 3 kez periyot geçilir yani 6 tane kök vardır.
2.
(k-2)/2 nin max değeri soruluyor.
diskriminanttan 8²-4.2.(k-2)>=0
(k-2)/2 en fazla 4 değeri almış olur.
3.
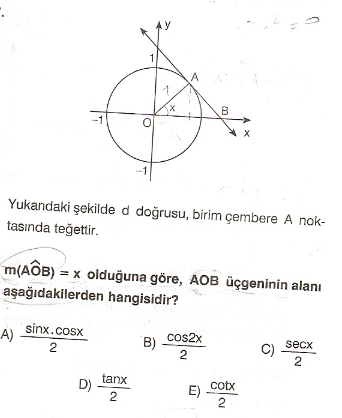
AB=tanx olur. dik kenarlar belli alan da (tanx)/2 olur.
5.
teğetin eğimi ile o noktadaki türev aynı verilmiş yani bu iki teğet aynı.
(1,0) ve (3,y) noktasından geçen teğetin eğimi 4 müş. buradan y=8 bulunur.
ayrıca tepe noktası yanılmıyorsam y ekseni üzerinde verilmiş yani kökler toplamı 0 yani fonksiyon ax²+c şeklinde.
parabol f=ax²+c olsun
f'(3)=a.2.3=6a=4
f(3)=9a+c=8 bulduk
9a=4.9/6=6 olacağından f(0)=c=2 bulunur.
sin x her periyotta 2 kez 1/2 değerini alacaktır. sin3x verildiğinden 3 kez periyot geçilir yani 6 tane kök vardır.
2.
(k-2)/2 nin max değeri soruluyor.
diskriminanttan 8²-4.2.(k-2)>=0
(k-2)/2 en fazla 4 değeri almış olur.
3.
AB=tanx olur. dik kenarlar belli alan da (tanx)/2 olur.
5.
teğetin eğimi ile o noktadaki türev aynı verilmiş yani bu iki teğet aynı.
(1,0) ve (3,y) noktasından geçen teğetin eğimi 4 müş. buradan y=8 bulunur.
ayrıca tepe noktası yanılmıyorsam y ekseni üzerinde verilmiş yani kökler toplamı 0 yani fonksiyon ax²+c şeklinde.
parabol f=ax²+c olsun
f'(3)=a.2.3=6a=4
f(3)=9a+c=8 bulduk
9a=4.9/6=6 olacağından f(0)=c=2 bulunur.
2.
şöyle bi çözüm de yapılabilir
köklerin toplamı -(-8)/2=4
toplamları 4 olan iki reel sayının çarpımı yani sorulan değer de en fazla (4/2)²=4 olabilir. (aritmetik orta≥geometrik orta)
şöyle bi çözüm de yapılabilir
köklerin toplamı -(-8)/2=4
toplamları 4 olan iki reel sayının çarpımı yani sorulan değer de en fazla (4/2)²=4 olabilir. (aritmetik orta≥geometrik orta)
