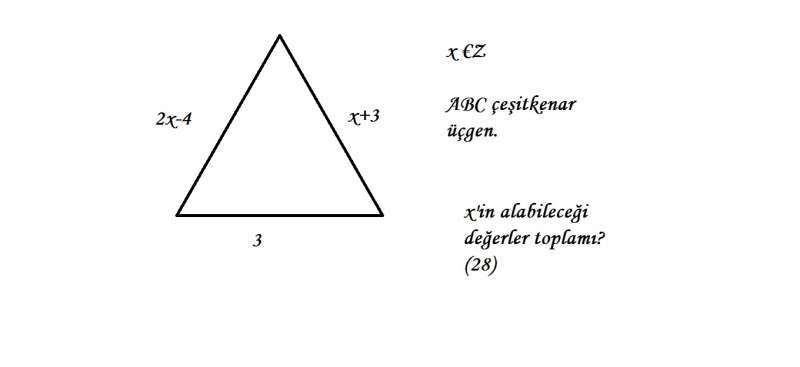
Bulduğum aralık: 4<x<10, toplam 35. Cevâbın 35 değil 28 olduğunu görünce düşündüm, aralıktaki '7' değerini kenarlarda yerine yazdım ve 2x-4=x+3, bu da çeşitkenar olmasına engel. 7'yi bu yüzden iptal etmeliyim, değil mi?
mesele yok o hâlde.
2
3
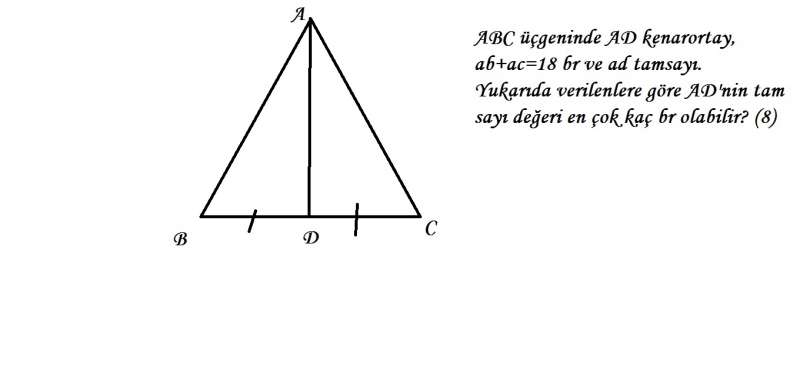
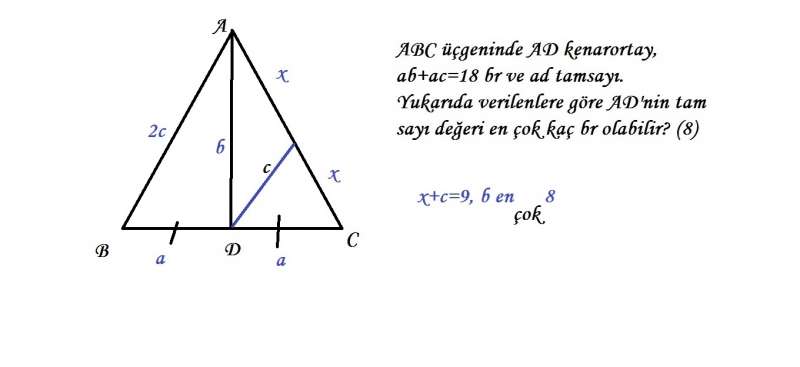
x tam sayı isteniyor sanırım, belirtmemişsin 
Evet dediğin şekilde 7 istenen x değerleri arasından çıkıyor
Evet dediğin şekilde 7 istenen x değerleri arasından çıkıyor
x tam sayı isteniyor sanırım, belirtmemişsin 
Evet dediğin şekilde 7 istenen x değerleri arasından çıkıyor
Evet dediğin şekilde 7 istenen x değerleri arasından çıkıyor
görüntüye dikkat et, yazdım oraya.
anlaşıldı teşekkür ettim
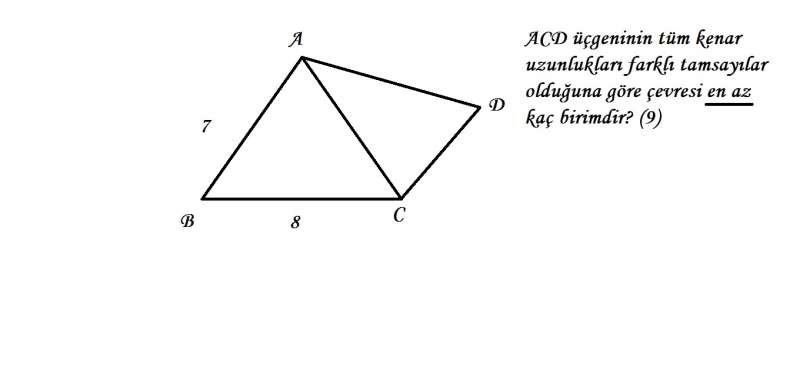
Üçgenin bir kenarı, diğer iki kenarın farkının mutlak değerinden büyük, toplamından küçük olmalıdır. Dolayısıyla |AC|=x olursa;
|8-7| < x < 8+7
1 < x <15
En az çevreyi istediğimiz için x en az 2 olabilir. ACD için yukarıdaki kurallara dikkat ederek kenar uzunlukları en az 2, 3 ve 4 olabilir. Dolayısıyla 2+3+4=9 olur.
1, 2, 3'ün yukarıdaki kurallara uymadığına dikkat edin.
İyi günler.
|8-7| < x < 8+7
1 < x <15
En az çevreyi istediğimiz için x en az 2 olabilir. ACD için yukarıdaki kurallara dikkat ederek kenar uzunlukları en az 2, 3 ve 4 olabilir. Dolayısıyla 2+3+4=9 olur.
1, 2, 3'ün yukarıdaki kurallara uymadığına dikkat edin.
İyi günler.
Üçgenin bir kenarı, diğer iki kenarın farkının mutlak değerinden büyük, toplamından küçük olmalıdır. Dolayısıyla |AC|=x olursa;
|8-7| < x < 8+7
1 < x <15
En az çevreyi istediğimiz için x en az 2 olabilir. ACD için yukarıdaki kurallara dikkat ederek kenar uzunlukları en az 2, 3 ve 4 olabilir. Dolayısıyla 2+3+4=9 olur.
1, 2, 3'ün yukarıdaki kurallara uymadığına dikkat edin.
İyi günler.
|8-7| < x < 8+7
1 < x <15
En az çevreyi istediğimiz için x en az 2 olabilir. ACD için yukarıdaki kurallara dikkat ederek kenar uzunlukları en az 2, 3 ve 4 olabilir. Dolayısıyla 2+3+4=9 olur.
1, 2, 3'ün yukarıdaki kurallara uymadığına dikkat edin.
İyi günler.
çok teşekkür ederim,,,
ımmm buldum

sinavkizi bari sen yapma ya 

Sorularını ilk mesaja ekle, sonra karışıklık oluyor şimdi ben birleştiriyorum mesajlarını
Sorularını ilk mesaja ekle, sonra karışıklık oluyor şimdi ben birleştiriyorum mesajlarını
sinavkizi bari sen yapma ya 

Sorularını ilk mesaja ekle, sonra karışıklık oluyor şimdi ben birleştiriyorum mesajlarını
Sorularını ilk mesaja ekle, sonra karışıklık oluyor şimdi ben birleştiriyorum mesajlarını
Biliyorum ama o zaman kimse görmüyor soruları  yukarıda kaldığı için yorumlarda görünmüyor diye böyle ekledimdi.
yukarıda kaldığı için yorumlarda görünmüyor diye böyle ekledimdi.
Soruların sonraki mesajlarda olması, daha sonra konuyu incelemek isteyen arkadaşlar için karışık gelebilir.
