1. Analitik düzlemde x²+y²=100 denklemi ile verilen çemberin içindeki A(3,4) noktasından geçen en kısa kirişin uzunluğu kaç birimdir? (10√3)
2. Analitik düzlemde x²+y²-8x+6y-75=0 denklemi ile verilen çembere dıştan teğet ve yarıçapı 2 br olan çemberlerin merkezlerinin geometrik yerinin denklemi nedir? ((x-4)²+(y+3)²=144
3. Anal. düzlemde verilen (x-2)²+(y-3)²=16 çemberinin orijin merkezli ve k=3 oranlı homotetiğinin denklemi nedir? ((x-6)²+(y-9)²=144
4. Anal. düzlemde verilen x²+y²-2x+4y+1=0 çemberinin u=(5,6) vektörü doğrultusunda ötelenmesi ile elde edilen çember denklemi nedir? (x-6)²+(y-4)²=4
2. Analitik düzlemde x²+y²-8x+6y-75=0 denklemi ile verilen çembere dıştan teğet ve yarıçapı 2 br olan çemberlerin merkezlerinin geometrik yerinin denklemi nedir? ((x-4)²+(y+3)²=144
3. Anal. düzlemde verilen (x-2)²+(y-3)²=16 çemberinin orijin merkezli ve k=3 oranlı homotetiğinin denklemi nedir? ((x-6)²+(y-9)²=144
4. Anal. düzlemde verilen x²+y²-2x+4y+1=0 çemberinin u=(5,6) vektörü doğrultusunda ötelenmesi ile elde edilen çember denklemi nedir? (x-6)²+(y-4)²=4
C.1
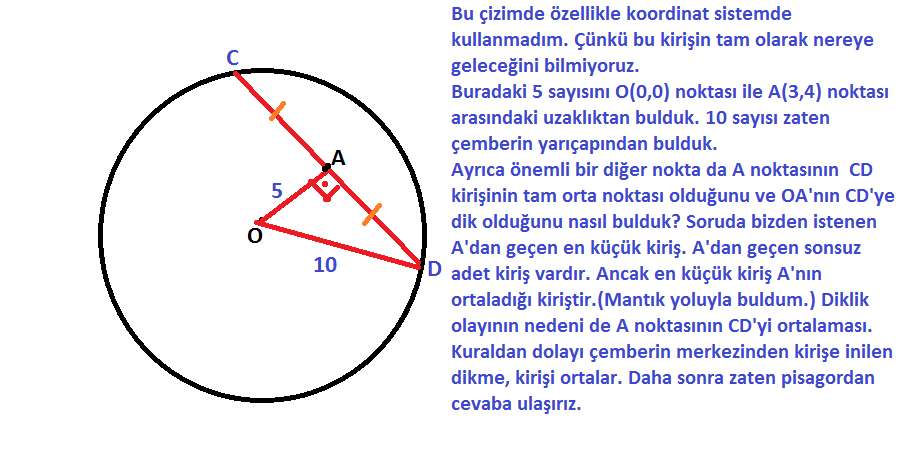
C.2
x²-8x+y²+3y-75=0 denklemini daha kullanışlı hale getirmeye çalışalım.
x²-8x+y²+3y=75
x²-8x+y²+3y+25=75+25
x²-8x+16+y²+3y+9=100
(x-4)²+(y+3)²=100
Bu denklemden anladık ki çemberimizin merkezi 10 cm imiş ve merkezi (4,-3) noktası imiş.
Şimdi sorulana bakalım. Bu çembere dıştan teğet, yarıçapları 2 cm olan çemberlerin merkezlerinin geo. yer denklemi sorulmuş.
Bu çemberlerin merkezlerini birleştirirsek, merkezi (4,-3) ve yarıçapı 12 cm olan yeni bir çember elde ederiz. Bu çemberin denklemi de;
(x-4)²+(y+3)²=144 şeklinde olur.
x²-8x+y²+3y-75=0 denklemini daha kullanışlı hale getirmeye çalışalım.
x²-8x+y²+3y=75
x²-8x+y²+3y+25=75+25
x²-8x+16+y²+3y+9=100
(x-4)²+(y+3)²=100
Bu denklemden anladık ki çemberimizin merkezi 10 cm imiş ve merkezi (4,-3) noktası imiş.
Şimdi sorulana bakalım. Bu çembere dıştan teğet, yarıçapları 2 cm olan çemberlerin merkezlerinin geo. yer denklemi sorulmuş.
Bu çemberlerin merkezlerini birleştirirsek, merkezi (4,-3) ve yarıçapı 12 cm olan yeni bir çember elde ederiz. Bu çemberin denklemi de;
(x-4)²+(y+3)²=144 şeklinde olur.
C.4
x²+y²-2x+4y+1=0 denklemini 2. soruda yaptığımız gibi kullanışlı hale getirirsek şöyle olur:
(x-1)²+(y+2)²=4
Bu denklemden anlıyoruz ki; çemberimiz, merkezi (1,-2) ve yarıçapı 2 cm olan bir çember.
Biz eğer bu çemberi u->(5,6) vektörü doğrultusunda taşırsak;
merkezi (1+5,-2+6)=(6,4), yarıçapı ise değişmeyeceği için 2 cm olacaktır. Bu çemberin denklemi de;
(x-6)²+(y-4)²=4 şeklinde olur.
x²+y²-2x+4y+1=0 denklemini 2. soruda yaptığımız gibi kullanışlı hale getirirsek şöyle olur:
(x-1)²+(y+2)²=4
Bu denklemden anlıyoruz ki; çemberimiz, merkezi (1,-2) ve yarıçapı 2 cm olan bir çember.
Biz eğer bu çemberi u->(5,6) vektörü doğrultusunda taşırsak;
merkezi (1+5,-2+6)=(6,4), yarıçapı ise değişmeyeceği için 2 cm olacaktır. Bu çemberin denklemi de;
(x-6)²+(y-4)²=4 şeklinde olur.
3. soruyu bilmiyorum çünkü homotetik ne demek acaba onu bilmiyorum. Ama soruya ve cevaba baktığımda şunu görüyorum ki;
(x-2)²+(y-3)²=16 çemberinin k=3 oranlı homotetiğini alırken; (x-2.3)²+(y-3.3)²=16.3²yaparız. Ama sadece bir tahmin yaptım, bilen birinin çözümünü yazmasında fayda var.
(x-2)²+(y-3)²=16 çemberinin k=3 oranlı homotetiğini alırken; (x-2.3)²+(y-3.3)²=16.3²yaparız. Ama sadece bir tahmin yaptım, bilen birinin çözümünü yazmasında fayda var.
2. soruda son kısımda iki denklem de nasıl aynı ldu?
2. soruda, dış teğet çemberlerin merkezlerini birleştirerek elde ettiğimiz yeni çemberle, baştaki çemberin merkezi aynı nokta olur. Bundan dolayı (x-4) ve (y+3) kısımları aynı olur iki denklemde de. Ancak bu iki çemberin yarıçapları farklı olduğundan denklemlerin son kısımları farklı oldu.
Duygu destek için teşekkür ederim. 
ama bunda 1 noktam var, homotetiyi nasıl uygulayacağım? 2. sınıfta görmedik homoteti, hiç bilmiyorum.
ama bunda 1 noktam var, homotetiyi nasıl uygulayacağım? 2. sınıfta görmedik homoteti, hiç bilmiyorum.Diğer çözümlü sorular alttadır.
Analitik Geometri Soruları Analitik Geometri Soruları ve Çözümleri Çember ile İlgili Çözümlü Sorular Çemberin Analitiği Çözümlü Sorular
Tüm Etiketler
Tüm Etiketler