hocam çok güzel bir yere parmak bastınız. benim de kafam çok karışıyor. Acaba bir nokta hem ekstremum hem dönüm noktası olabiliyor mu?
2)


3)


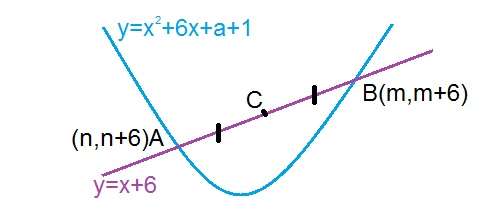

5)


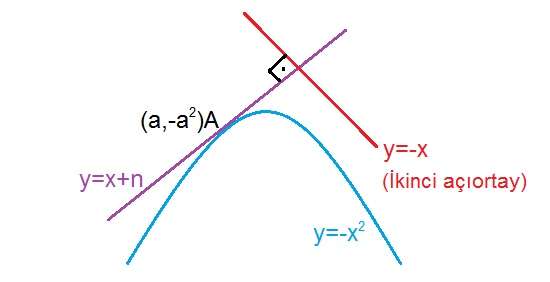
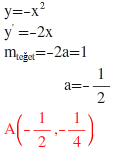
hocam f in türevinin grafiği verilmiş. c noktası ekstremum nokta olamaz ki grafikte teğet.
Aynı zamanda, c noktası, f'(x) in yerel ekstremum noktası olduğundan , f(x) in, büküm noktasıdır.
Tahminimce, c noktasında, f'(x), x e teğet değil, x e değmeden dönüp gidiyor. O zaman c, sadece büküm noktası olur.
Aynı anda hem büküm , hem ekstremum noktası olması zor gibi.
Yalnız şu var. Çizdiğim, f(x) in grafiğinde, x=c noktasında, fonksiyona teğet çizilebilir gibi duruyor. Aynı zamanda büküm noktası da,
O zaman şu ihtimal çıkıyor. Bir nokta da, f'(x)=0 ve, f''(x)=0 olabilir. Bu noktada, büküm noktası olur ama, f'(x)=0 olmasına rağmen, o nokta ekstremum nokta olmayabilir.
Süleyman Hocam çok teşekkürler emeğinize sağlık 
