1)
işleminin sonucu kaçtır?
a)200
b)201
c)204
d)207
e)209
2)m ve n farklı iki pozitif tamsayı
m.n=11(m-n)
olduğuna göre, m+n toplamı kaçtır?
a)70
b)90
c)110
d)120
e)130
3)
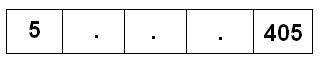
Yukarıdaki şekilde bulunan boş karelerde birer tamsayı bulunmaktadır.Boş karelerdeki her sayı,kendisinden bir önceki ve bir sonraki karelerde bulunan sayıların geometrik ortalamasına eşittir.
Buna göre,boş karelerde bulunan sayıların toplamı kaçtır?
a)325
b)215
c)195
d)60
e)45
4)
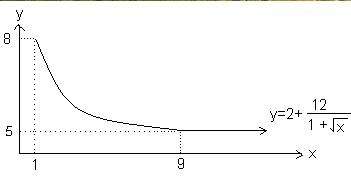
Yukarıdaki grafik x adet mal için ödenen miktarı gösteriyor.
Buna göre,bir seferde 121 adet mal alıp bu malın tanesini 8TL den satan tüccarın karı kaç TL dir?
a)600
b)605
c)615
d)620
e)630
[doğru cevap B]
5)
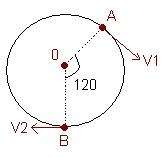
O merkezli dairesel pistte A ve B noktalarından hızları V1 ve V2 olan araçlar aynı anda şekildeki gibi hareket etmektedir.
V1<V2 olmak üzere iki araç 6 dakika sonra ilk kez yanyana geldiklerine göre harekete başladıktan kaç dakika sonra 7. kez yanyana gelirler?
a)42
b)48
c)52
d)54
e)60
[cevap E]