kırmızı gece 19:32 26 Ağu 2013 #1
merhaba
3)Aşağıdakilerden sayılardan hangisi her zaman bir rasyonel sayıdır?
a)(x-7)/3 b)(2x-1)/(x²+3) c) (x+5)/(x³+8) d)(x²-16)/(x²+16) e) 10/(x⁴+1)
4) x ve y aralarında asal sayılar olmak üzere
olduğuna göre x+y toplamı en az kaçtır?
a) 41 b) 38 c) 24 d) 5 e)4
5) 1/7<a<b<c<2/7 olduğuna göre a,b,c asayıları sırasıyla aşağıdakilerden hangisi olabilir?
a) 3/28,5/28,7/28 b) 12/63,15/63,17/63 c) 6/35,8/35,11/35 d) 7/56,13/56,18/56
e)7/42,10/42,14/42
3)Aşağıdakilerden sayılardan hangisi her zaman bir rasyonel sayıdır?
a)(x-7)/3 b)(2x-1)/(x²+3) c) (x+5)/(x³+8) d)(x²-16)/(x²+16) e) 10/(x⁴+1)
4) x ve y aralarında asal sayılar olmak üzere
1
9
<
x
y
<
5
12
olduğuna göre x+y toplamı en az kaçtır?
a) 41 b) 38 c) 24 d) 5 e)4
5) 1/7<a<b<c<2/7 olduğuna göre a,b,c asayıları sırasıyla aşağıdakilerden hangisi olabilir?
a) 3/28,5/28,7/28 b) 12/63,15/63,17/63 c) 6/35,8/35,11/35 d) 7/56,13/56,18/56
e)7/42,10/42,14/42
5.soru
şıklardan git.
a) payda 28 olduğu için eşitsizlikte paysa eşitle.
4/28<a<b<c<8/28. a sayısı 4/28'den büyük olmak zorunda ama şıkta 3/28 değeri almış. a şıkkı olmaz.
böyle böyle her şıkkı deneyin. cevap b şıkkı.
şıklardan git.
a) payda 28 olduğu için eşitsizlikte paysa eşitle.
4/28<a<b<c<8/28. a sayısı 4/28'den büyük olmak zorunda ama şıkta 3/28 değeri almış. a şıkkı olmaz.
böyle böyle her şıkkı deneyin. cevap b şıkkı.
kırmızı gece 13:14 27 Ağu 2013 #4
cevaplar için teşekkürler, 2, 3 ve 4. soru için günceldir..
2.soru gene aynı yolla yapacaksınız.
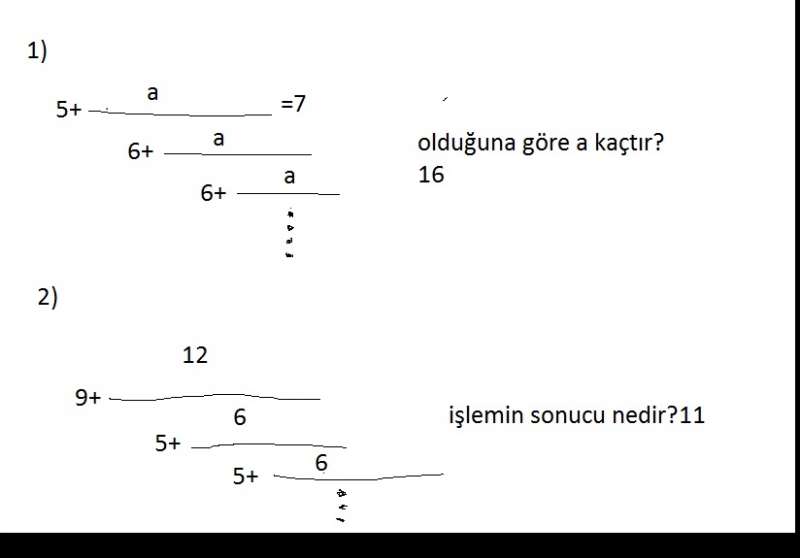
çözüm 1!
bu tür çözümlerde x'in pozitif değeri alınır. çünkü pozitif bir sayı ile gene pozitif bir sayıyı topluyorsunuz.(5+6/5+6/....)
çözüm 2!
çözüm 1!
bu tür çözümlerde x'in pozitif değeri alınır. çünkü pozitif bir sayı ile gene pozitif bir sayıyı topluyorsunuz.(5+6/5+6/....)
çözüm 2!
3.soru b şıkkı mı? tüm şıkları denedim.
a)x=7 olduğunda 0 olur.
c)x=-5 olduğunda 0 değerini alır.
d)x=0'da -1,x=+4,-4 değerlerinde 0 değerini alır.
e)x=0 değerinde 10 çıkar sonuç.
a)x=7 olduğunda 0 olur.
c)x=-5 olduğunda 0 değerini alır.
d)x=0'da -1,x=+4,-4 değerlerinde 0 değerini alır.
e)x=0 değerinde 10 çıkar sonuç.
kırmızı gece 13:20 28 Ağu 2013 #7
teşekkürler 4 için güncel
4.soru
cevap 4 mü? bir kontrol eder misiniz?
cevap 4 mü? bir kontrol eder misiniz?
4.soru
kural; m,n,z,v aralarında asal sayılar.
m/n=z/v ise
m=z ve n=v olur.
payda eşitleyin.
1/9<x/y<5/12
9 ve 12 paydaları en küçük 36'da eşitlenir. bizden en küçük x+y değerini istediği için y'ninde 36'ya eşitlenebildiğini farz edelim.
4/36<x.k/y.k<15/36
1/9'u 4 ile, 5/12 ise 4 ile genişlettim.
x/y'yi de k değeri ile genişlettim.(y'nin tam değerini bilmediğim için böyle yaptım. sonuçta hepsi sadeleşince gene aynı değerler çıkar)
x.k/y.k 4/36 ile 15/36 arasında olmalı. ve bu değerler aralarında asal olmamalı.çünkü k çarpanı var. o zaman
x.k/y.k değeri;
6/36,8/36,10/36 ve 12/36 değerleri alır. hepsini sadeleştirin;
1/6, 2/9, 5/18 ve 1/3 değerleri çıkar. bunlar x/y değerleri. x ve y aralarında asal oldukları için yukarıdaki kuralı uygularsakİ
x'in çözüm kümesi {1,2,5} olur.
y'nin çözüm kümesi{3,6,8,9} eder.
x+y'nin en küçük değeri
1+3=4
kural; m,n,z,v aralarında asal sayılar.
m/n=z/v ise
m=z ve n=v olur.
payda eşitleyin.
1/9<x/y<5/12
9 ve 12 paydaları en küçük 36'da eşitlenir. bizden en küçük x+y değerini istediği için y'ninde 36'ya eşitlenebildiğini farz edelim.
4/36<x.k/y.k<15/36
1/9'u 4 ile, 5/12 ise 4 ile genişlettim.
x/y'yi de k değeri ile genişlettim.(y'nin tam değerini bilmediğim için böyle yaptım. sonuçta hepsi sadeleşince gene aynı değerler çıkar)
x.k/y.k 4/36 ile 15/36 arasında olmalı. ve bu değerler aralarında asal olmamalı.çünkü k çarpanı var. o zaman
x.k/y.k değeri;
6/36,8/36,10/36 ve 12/36 değerleri alır. hepsini sadeleştirin;
1/6, 2/9, 5/18 ve 1/3 değerleri çıkar. bunlar x/y değerleri. x ve y aralarında asal oldukları için yukarıdaki kuralı uygularsakİ
x'in çözüm kümesi {1,2,5} olur.
y'nin çözüm kümesi{3,6,8,9} eder.
x+y'nin en küçük değeri
1+3=4
kırmızı gece 23:13 30 Ağu 2013 #10
teşekkürler...............