kırmızı gece 17:26 16 May 2012 #1
merhabalar
1) 1/8<a<1/4
1/9<b<1/2
olduğuna göre
ifadesinin alabileceği en büyük sayı değeri kaçtır? cvp:16
2)%5E%7B2%20%5Ccdot%20x%2B8%7D%3E16)
olduğuna göre x'in alabileceği en büyük x tam sayısı kaçtır?( ben cevabı -5 buluyorum, cevap anahtarında -7 )
3) a, b, c ,d ardışık çift sayılardır. Buna göre.(b%2Bd)%7D%7B4%20%5Ccdot%20b.c%7D%20)
oranı kaçtır? cvp:1
4)
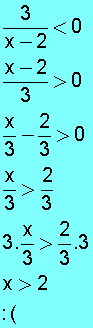
eşitsizliğini sağlayan x doğal sayılarının toplamı kaçtır? bu soruyu değer vermeden çözmeye çalıştığımda çözemedim. Hatamın nerede olduğunu bulamadım. şu şekilde çözdüm;
1) 1/8<a<1/4
1/9<b<1/2
olduğuna göre
ifadesinin alabileceği en büyük sayı değeri kaçtır? cvp:16
2)
olduğuna göre x'in alabileceği en büyük x tam sayısı kaçtır?( ben cevabı -5 buluyorum, cevap anahtarında -7 )
3) a, b, c ,d ardışık çift sayılardır. Buna göre
oranı kaçtır? cvp:14)
eşitsizliğini sağlayan x doğal sayılarının toplamı kaçtır? bu soruyu değer vermeden çözmeye çalıştığımda çözemedim. Hatamın nerede olduğunu bulamadım. şu şekilde çözdüm;
Cevap 3.
sayılar sırasıyla
2n
2n+2
2n+4
2n+6 olsun, yerine yazıp ortak paranteze alınca hemen çıkıyor.
Cevap 2.
0.5=5/10=1/2=2^(-1)
2^(-2x-8)>2^4
-2x-8>4
-2x>12 (her iki tarafı -2'ye bölünce yön değiştirecek:
x<-6, -6'dan küçük negatif ilk sayı (-7)
sayılar sırasıyla
2n
2n+2
2n+4
2n+6 olsun, yerine yazıp ortak paranteze alınca hemen çıkıyor.
Cevap 2.
0.5=5/10=1/2=2^(-1)
2^(-2x-8)>2^4
-2x-8>4
-2x>12 (her iki tarafı -2'ye bölünce yön değiştirecek:
x<-6, -6'dan küçük negatif ilk sayı (-7)
kırmızı gece 20:29 16 May 2012 #3 son soruda, takla atınca neden yön değiştirdi ki?
Cevap 3.
sayılar sırasıyla
2n
2n+2
2n+4
2n+6 olsun, yerine yazıp ortak paranteze alınca hemen çıkıyor.
Cevap 2.
0.5=5/10=1/2=2^(-1)
2^(-2x-8)>2^4
-2x-8>4
-2x>12 (her iki tarafı -2'ye bölünce yön değiştirecek:
x<-6, -6'dan küçük negatif ilk sayı (-7)
Cevap 3.
sayılar sırasıyla
2n
2n+2
2n+4
2n+6 olsun, yerine yazıp ortak paranteze alınca hemen çıkıyor.
Cevap 2.
0.5=5/10=1/2=2^(-1)
2^(-2x-8)>2^4
-2x-8>4
-2x>12 (her iki tarafı -2'ye bölünce yön değiştirecek:
x<-6, -6'dan küçük negatif ilk sayı (-7)
kırmızı gece 20:40 16 May 2012 #4
teşekkürler sınav kızı yardımların için....
Estağfurullah her zaman, 
da kalan ikisine aklım takılmadı değil.
da kalan ikisine aklım takılmadı değil. 
C.1
şeklinde olur.
Soruya bakarsak a ve b sayıları hakkında bir eşitsizlik verilmiş. Biz de bu eşitsizliklerden yararlanarak 1/a ve 1/b hakkında eşitsizliklere ulaşabiliriz. Peki nasıl?
Bu kuralı önce a için uygulayalım.
Şimdi de b için uygulayalım.
Soruda bizden istenene ulaşmak için bu iki eşitsizliği toplayalım.
O halde en büyük tam sayı değeri de 16 olur.
a+b
c
=
a
c
+
b
c
Bu kurala göre
a+b
a.b
kesrinin eşitini yazalım.
1
b
+
1
a
şeklinde olur.
Soruya bakarsak a ve b sayıları hakkında bir eşitsizlik verilmiş. Biz de bu eşitsizliklerden yararlanarak 1/a ve 1/b hakkında eşitsizliklere ulaşabiliriz. Peki nasıl?
"a<b ve a.b>0 ise
1
a
>
1
b
" bu kurala göre.
Bu kuralı önce a için uygulayalım.
8>
1
a
>4
olur.
Şimdi de b için uygulayalım.
9>
1
b
>2
olur.
Soruda bizden istenene ulaşmak için bu iki eşitsizliği toplayalım.
17>
1
a
+
1
b
>6
olur.
O halde en büyük tam sayı değeri de 16 olur.
4)
Eşitsizliğimizin tek kökü x=2'dir.
_________2_________
----------|++++++++
ifademiz 0'dan küçük olacağı için negatif kısmı alırız yani;
x<2 diye düşünüyorum.
x>2 olursa eşitsizlik asla sağlanmaz.
Eşitsizliğimizin tek kökü x=2'dir.
_________2_________
----------|++++++++
ifademiz 0'dan küçük olacağı için negatif kısmı alırız yani;
x<2 diye düşünüyorum.
x>2 olursa eşitsizlik asla sağlanmaz.
C.4
Sen çözümünde
Mesela 0'dan küçük bir sayı söyleyelim:
Sorunun asıl çözümü şöyle:
3/(x-2) negatifse, "x-2" de negatiftir. Bundan dolayı x-2<0 olur. Buradan da x<2 olur. Bunu sağlayan x doğaş sayıları {0,1} olur.
Sen çözümünde
3
x-2
<0 ise
x-2
3
>0 'dır, yazmışsın ama burası yanlış olmuş. Haliyle diğer işlemlerde sıkıntı olmasa bile cevap yanlış çıkmış.
Mesela 0'dan küçük bir sayı söyleyelim:
-1
2
<0'dır.Ama -2>0 dersek yanlış olur.
Sorunun asıl çözümü şöyle:
3/(x-2) negatifse, "x-2" de negatiftir. Bundan dolayı x-2<0 olur. Buradan da x<2 olur. Bunu sağlayan x doğaş sayıları {0,1} olur.
kırmızı gece 23:00 16 May 2012 #9
açıklamalarınız için teşekkürler arkadaşlar....
açıklayıcı oldu benim için
açıklayıcı oldu benim için