Karışık Sorular

1.
( x+y+z )=0
x.y.z=2
(x+y-z).(x-y+z).(y+z-x)=?

2.
t²=t-1
t⁵=?
Cvp : 1-t

3.
x⁴+x²+1=0 ifadesinin çarpanlarından biri hangisidir?
Cvp : x²-x+1

4.


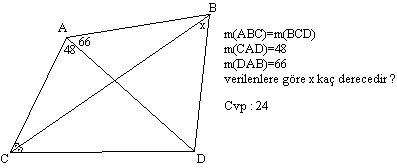
5.

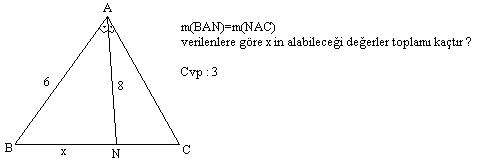
cevap1.

( x+y+z )=0
x.y.z=2
(x+y-z).(x-y+z).(y+z-x)=?

x+y=(-z)
(y+z)=(-x)
(x+z)=(-y)

bunları yerine yazalım

(-2z).(-2y).(-2x)=(-8).(x.y.z)=(-8.2)=(-16)

Cevap 2.

2.
t²=t-1
t⁵=?
Cvp : 1-t

t⁵=t².t².t
=(t-1).(t-1).(t)
dağıtalım gelir

c.3=)x⁴+x²+1=)x⁴+x²+1+x²-x²(+x² - x² ekleyelim)
=)x⁴+2x²+1-x²
=)(x²+1)²-x²
=)(x²-x+1)*(x²+x+1) çarpanları

(t²-2.t+1).t
t³-2.t²+t
buradan (1-t) nasıl çıkar anlayamadım galiba cevap anahtarında problem var

(t²-2.t+1).t'de t² yerine yine (t-1) yazın, sonra yine bir t² gelecek, onda da yerine yazın (1-t) yanıtı geliyor.
olmadı yazarım.

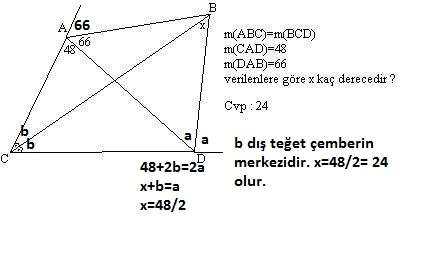
dış teğet çemberin merkezi olunca nasıl açıortaylık oluyordu?

Şekilde çizdiğim gibi 3 açı da açıortayla bölünüyor.

Bir iç açıortay var. Sonradan dışarıdaki açıda 66 bulunuyor. Böylece bir dış açı bir iç açı oluyor. 2 özellik varsa 3.de olmak zorundadır. O yüzden diğer açılarda açıortay oluşturur. Bundan ötürü B dış teğet çemberinin merkezidir.