küme

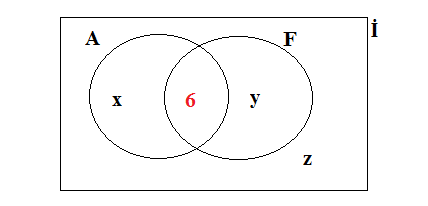
1)30 kişilik bir sınıfta öğrenciler matematik ve türkçe derslerinden en az birinden geçmişlerdir.matematikten geçenler türkçeden geçenlerin 4 katıdır.Her iki dersten de geçen en az bir kişi vardır. buna göre sadece türkçe dersinden geçen kaç kişi vardır?cevap:2


2)32 kişilik bir sınıfta herkes ingilizce bilmektedir.Almanca bilmeyen 20 kişi fransızca bilmeyen 18 kişidir.her üç dili de bilen 6 kişi olduğuna göre yalnız iki dili bilen kaç kişi vardır?cevap:14


3)32 kişilik bir sınıfta matematikten başarılı olan bütün öğrencile türkçeden de başarılıdır.matematikten başarılı olanların sayısı türkçeden başarılı olanalrın sayısının %40 dır.7 öğrenci her iki derstende başarısız olduğuna göre sadece türkçeden başarılı olan öğrenci sayısı kaçtır?cevap:15

1)
Bu tür sorularda kümeleri yuvarlak şekiller içerisinde çizerek göstermeniz çok yararlı olacaktır.Ben cebirsel olarak şöyle ifade etmeye çalışayım;

s(M/T)=x
s(MnT)=y
s(T/M)=z olsun.

Geri dönüp soruyu okursak;
x+y+z=30 bilgisinin verildiğini,
Aynı zamanda da
x+y=4(y+z)
x=3y+4z bilgisinin verildiğini,

Bu bilgiler ışığında hareket ederek,
4y+5z=30 ifadesine ulaşabileceğimizi görüyoruz.

Burada y>0 , z>0 olduğu soruda açıkça beyan edilmiş.
Bu şartı sağlayan tek durumun ise,z=2 ve y=5 için olduğunu kısa bir işlemle teyid ederek z=2 buluruz.

3)
Tıpkı birinci soruda yaptığımız gibi şekillerle ifade etmeye çalışalım;
s(M/T)=x
s(MnT)=y
s(T/M)=z olsun.
Bunların dışındaki boşluklu alanı ise t olarak ifade edelim.(Her iki dersten de başarısız olanlar)

Ayrıca soruda t=7 verilmiş.O halde;
x+y+z=25 bulunur.

Geri dönüp ifadeleri okuduğumuzda, x+y=4k alırsak y+z=10k alabileceğimiz sonucuna ulaşabiliriz.


Buradan sonra yapacağımız şey de aynen bir önceki sorudaki gibi...
Diğer soru sizde

2)

x+y+z+6=32 x+y+z=26
y+z=20
x+z=18
x+y+2z=38
x+y+z=26
z=12
x+y=14

.9. sınıf Kümeler Çözümlü Sorular Küme Problemleri ve Çözümleri küme soruları
Tüm Etiketler