Sorular

1. 3-|x-1|
________ >0 eşitsizliğini sağlayan tamsayıların toplamı kaçtır?
|x²-3x+2|

2. 24
__________ ifadesinin en büyük değeri kaçtır?
|x-3|+|x+1|

3. x²+x=3.|x| denklemini sağlayan tamsayıların toplamı kaçtır?

4. |x²-10x+25|=81 denklemini sağlyan x değerlerinin toplamı kaçtır?

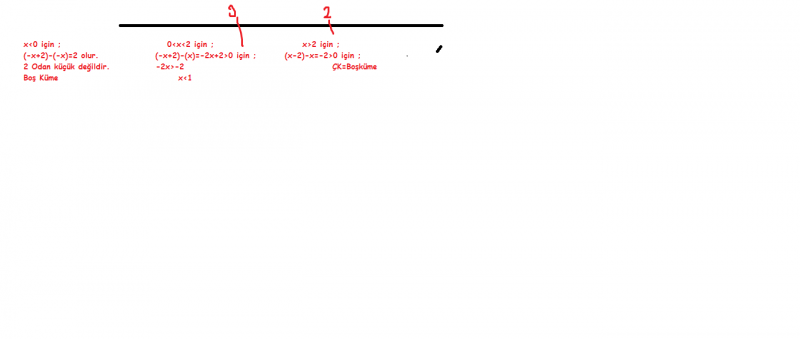
5.|x-2|-|x|>0 ise x hangi aralıkta bulunmaktadır?

Teşekkürler.

C-4

|(x-5)²|=9²

|x-5|=9

x=14
x=-4 olarak bulunur.
Toplamları 14-4=10 olacaktır.

C-3

x=0
x>0
x<0 için durumları inceleyelim.

x=0 için sağlanıyor. Ancak toplama bir etkisi yok.

x>0 için,

x²+x=3x
x²-2x=0
x(x-2)=0
x=0
x=2

x<0 için

x²+x=-3x
x²+4x=0
x(x+4)=0
x=0
x=-4

Bulduğumuz x değerleri 0, 2 ve -4.
Toplamları -2 olacaktır.

2.Soru

İfadenin en büyük olması için payda en küçük olmalıdır.
|x-3|+|x+1| ifadesinin en küçük değeri için her birini teker teker sıfıra eşitleyelim.
x-3=0 => x=3
x+1=0 => x=-1
Teker teker yerlerine koyarsak |3-3|+|-1-3|=4 ve |-1-3|+|1-1|=4 olur.

Her ikiside aynı oldu ; 24/4=6 olur.

C-2

Kesrin paydası en küçük değerini almalıdır.

Paydadaki mutlak değerlerden birini 0'a eşitleyelim,
x-3=0
x=3 için işlem yapalım. (Diğerini sıfıra eşitleyip x=-1 için işlem yapsak da aynı sonuca ulaşırız)

24/|0|+|4|
24/4=6 en büyük değeri olacaktır.

5.|x-2|-|x|>0 ise x hangi aralıkta bulunmaktadır?

Doğruyu parçalarsak ;


-------------------------0--2----------------- şeklinde olur.
x<0 için ;
(-x+2)-(-x)=2 olur.
2 Odan küçük değildir.
Boş Küme

---------------------------------
0<x<2 için ;
(-x+2)-(x)=-2x+2>0 için ;
-2x>-2
x<1

---------------------------------

x>2 için ;
(x-2)-x=-2>0 için ;
ÇK = BOŞKÜME

X'in aralığı = ÇK=(-∞,1)

3-|x-1|
________ >0 eşitsizliğini sağlayan tamsayıların toplamı kaçtır?
|x²-3x+2|

|x²-3x+2|=|x-2|.|x-1| Mutlaka pozitif olacaktır O halde pay da pozitif olursa şartımız sağlancaktır.
3-|x-1|>0 ;
3>|x-1|
3>x-1>-3
4>x>-2 olur.
x={3,2,1,0,-1}
3 olur.
2 olmaz.(Paydaya bakarsan sağlamaz.)
1 olmaz.(Paydaya bakarsan sağlamaz.)
0 olur.
-1 olur.

3+(-1)=2 olur.