Acil Soru yardımı !!!

Birkaç sorum var. Bakabilirseniz çok sevinirim.

1) -3<a<4 ise 3a-2 'nin tam sayı değerleri toplamı nedir?


2) -3<a<6
b+a²=6 b'nin alacağı kaç tam sayı değeri vardır?


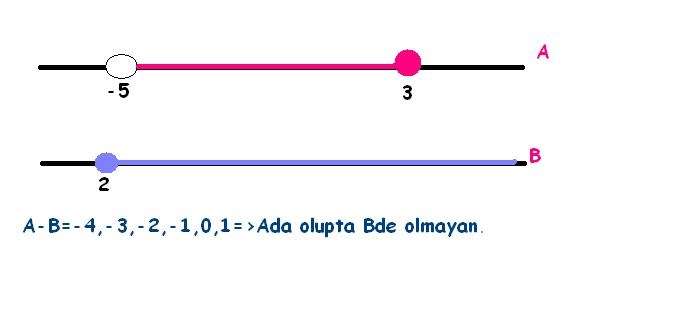
3) A= (-5, 3] ve B= [2 , ∞) ise A-B nedir?


4) x,y,z gerçek sayıları için x<y<z ve x+y+z=3 ise hangileri doğrudur?
I. x<1 II. y<1 III. z>1 IV. y+z>2 V. x+y>2


5) Küpü kendisinden küçük olan gerçek sayıları içeren aralık hangisinde verilmiştir?
A) (0,1) B) (-1,1) C) (-∞, 1) ∪ (0,1) D) (-∞, 1) E) (-1, ∞)


Yukarıdaki soruların çözümlerini yazabilirseniz çok mutlu olurum. Şimdiden teşekkürler...

C.1
-3<a<4 ise
-9<3a<12
-11<3a-2<10
3a-2=-10,-9......0,.....9=-10

C.2
-3<a<6 ise 0≤a²<36
b+a²=6 ise b=6-a²
0≤a²<36 ise
0≥-a²>-36
6≥6-a²>-30
6≥b>-30
b=6,5,4,....0,-1,.....-29=36 tane

C.3



C.4

x=y=z farz edelim.
x+y+z=3=3y
y=1 x<1<z

Bu durumda;
1.x<1 doğrudur.
2. y=1 olduğu için yanlıştır.
3.z>1 doğrudur.
4. y+z>2 doğrudur. çünkü z>1 ve y=1 olduğu için 1+z>2 dir.
5. x+y>2 yanlıştır. çünkü x<1 ve y=1 olduğu için x+y<2 dir.
1-3-4 doğrudur.

melek yanlışlık yapmıyorsam ilk soruda sağ sınır 10 olmalı

Evet hocam

C.5
x³<x
x³-x<0
x(x²-1)<0
x.(x+1)(x-1)<0
x<1
x<-1
0<x<1

(-∞,-1)u(0,1)

Melek12 cevaplar için çok teşekkür ederim. Çok işime yaradılar. Mümkün olsaydı 5'ten fazla soru yazacaktım ama site bildiğin gibi 5'den fazlasına izin vermiyor.
Yalnız iki sorum olacak;

İlk olarak 2. soruda neden "-3<a<6 ise 0≤a²<36" dedin? Yani hepsinin karesini alırken -3 neden 0 oldu ve < , ≤ e dönüştü?

Bir de 5. soruda x.(x+1)(x-1)<0 dan sonra nasıl x<1 , x<-1 , 0<x<1 bulduk?


Bu soruların da cevaplarını yazabilirsen çok mutlu olurum. Şimdiden çok teşekkürler...

Nasıl anlatsam bilmiyorum. :S Nasıl işliyorsunuz bu konuyu onu da bilmiyorum. O yüzden kafanın karışmaması adına öğretmenine danışman daha yerinde olacaktır.

Peki çok teşekkürler.

İlk olarak 2. soruda neden "-3<a<6 ise 0≤a²<36" dedin? Yani hepsinin karesini alırken -3 neden 0 oldu ve < , ≤ e dönüştü?
Bu soruna binaen;
-3<a<6 ise a² alabileceği en yüksek değer 36'dır. Fakat alabileceği en küçük değere biraz daha dikkatli bakalım. a'nın 0 değeri alabildiğini görüyoruz. Bu tarz sorularda öğrencileri en çok çelişkiye düşüren kare alırken alt sınırın karesini almaktır.
a=0 olabilecekken alt sınıra 9 yazamayız. Bir tam sayının karesi daima doğal sayıdır. Bunları üst üste koyup yargı koyarsak a² değerimiz 0'a eşit veya 0'dan büyük olabilir. Bunun matematik diliyle yazımı da 0≤a² olacağı için burada bu şekilde yazdık.

Bir de 5. soruda x.(x+1)(x-1)<0 dan sonra nasıl x<1 , x<-1 , 0<x<1 bulduk?
Bu soruna binaen de;
x.(x+1).(x-1)<0 ise bu ifadeyi 0'a eşitleyen değerleri buluruz önce. O değerler de;
x= 0, x=-1, x=1 için ifademizin 0'a eşit olduğunu gördük. Bu değerler kritik değerlerdir. Bu değerler etrafında x değerimiz hakkında yorum yapalım şimdi;
Fakat eşitsizliğimizde ifademizin 0'dan küçük olması gerektiğini görüyoruz.
x değerimizin (-1)'den daha küçük olduğu değerler için ifademizi ele alalım;
x--> negatif bir ifade olur(x<-1 ise x negatiftir)
x+1--> negatif bir ifade olur(x<-1 ise x+1<0)
x-1--> negatif bir ifade olur(x<-1 ise x-1<-2)
x.(x+1).(x-1) işlemimizin işaretleri: (-).(-).(-) oldu bu durumda çarpım negatiftir
x<-1 için eşitsizliğimiz sağlanıyor.
x değerimizin (-1)'den büyük 0'dan küçük olduğu değerler için ifademizi ele alalım;
x--> negatif bir ifade olur(-1<x<0 ise x negatiftir)
x+1--> pozitif bir ifade olur(-1<x<0 ise 0<x+1<1)
x-1--> negatif bir ifade olur(-1<x<0 ise -2<x-1<-1)
x.(x+1).(x-1) işlemimizin işaretleri: (-).(+).(-) oldu bu durumda çarpım daima pozitiftir.
-1<x<0 için eşitsizliğimiz sağlanmıyor.
x değerimizin 0'dan büyük 1'den küçük olduğu değerler için ifademizi ele alalım;
x--> pozitif bir ifade olur(0<x<1 ise x pozitiftir)
x+1--> pozitif bir ifade olur(0<x<1 ise 1<x+1<2)
x-1--> negatif bir ifade olur(0<x<1 ise -1<x-1<0)
x.(x+1).(x-1) işlemimizin işaretleri: (+).(+).(-) oldu bu durumda çarpım daima negatiftir.
0<x<1 için eşitsizliğimiz sağlanıyor.
x değerimizin 1'den büyük olduğu değerler için ifademizi ele alalım;
x--> pozitif bir ifade olur(1<x ise x pozitiftir)
x+1--> pozitif bir ifade olur(1<x ise 2<x+1)
x-1--> pozitif bir ifade olur(1<x ise 0<x-1)
x.(x+1).(x-1) işlemimizin işaretleri: (+).(+).(+) oldu bu durumda çarpım daima pozitiftir.
1<x için eşitsizliğimiz sağlanmıyor.

frk anlatımın için çok teşekkür ederim. Şimdi daha iyi anladım. Ancak kafamı kurcalayan son bir şey var. Bir tarafı negatif olan eşitsizliklerde eşitsizliğin karesini alırken her zaman 0 mı yazmak zorundayız? Yani;
-2<a<5 ise bunun karesi --> 0≤a<25 mi olur? Ya da,
-10<a<4 ise bunun karesi gene --> 0≤a<16 mıdır? Son olarak da,
-20<a<-5 gibi eşitsizliklerin karelerini nasıl alırız?