Eğim

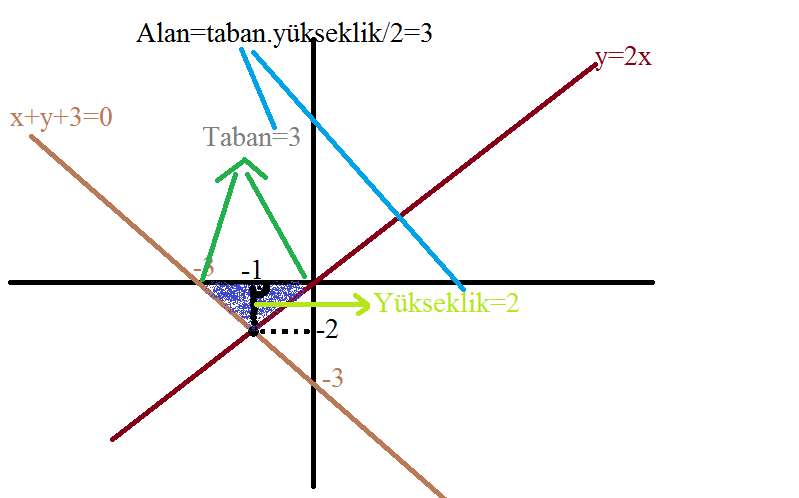
y=2x, x+y+3=0 doğruları ve x ekseni arasında kalan üçgensel bölgenin alanı kaç birim karedir ?

2-Eğimi -2 olan ve A(1,3) noktasından geçen doğru denklemi nedir ?

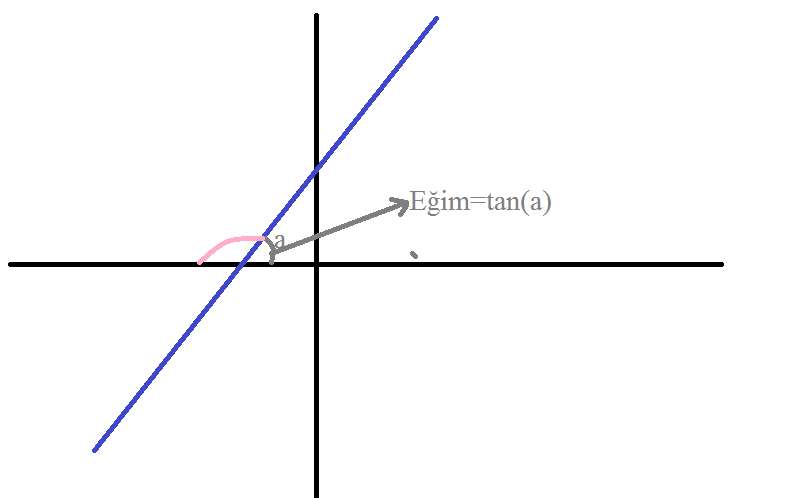
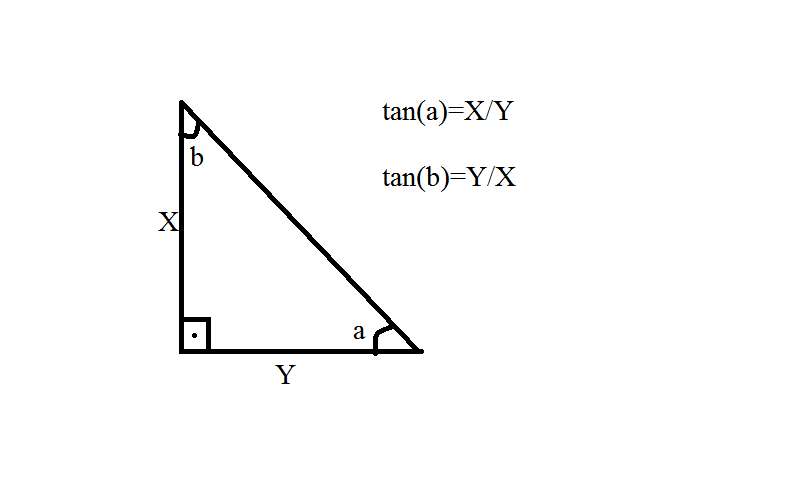
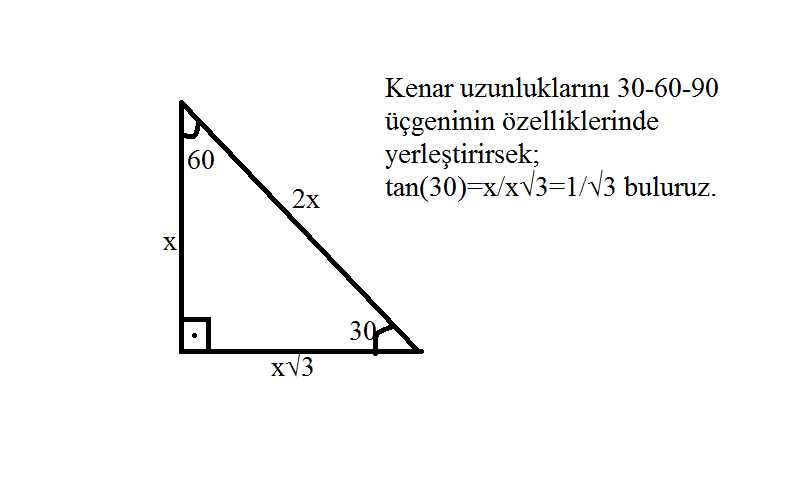
3-x ekseni ile pozitif yönde 30'lik açı yapan ve başlangıç noktasından geçen doğrunun denklemi nedir ?

C.1
y=2x doğrusu için önce x=0 verirsek y=0 buluruz. O halde doğru orijinden geçmeli.
x+y+3=0 doğrusu için x=0 verirsek y=-3 buluruz, y=0 için de x=-3 buluruz. O halde doğru (0,-3) ve (-3,0) noktalarından geçmeli.
Şimdi de bu iki doğrunun kesişim noktasını bulalım. Bunun için de bu iki denklemi ortak çözeceğiz.
y=2x ve x+y+3=0 denklemlerini yok etme metoduyla değil de yerine koyma metoduyla daha rahat çözeri. Bunun 2. denklemde y gördüğümüz yere 2x yazacağız. Şöyle olur: x+2x+3=0 Buradan x=-1 olur. y=2x'di. Bunun için de y=-2 buluruz.
Şimdi bu iki doğruyu bunlara göre çizelim.

C.2
Eğimi m olan ve (a,b) noktasından geçen doğrunun denklemi y-b=m(x-a) şeklindeydi. Buna göre eğimi=m=-2 ve geçtiği nokta (1,3) olan doğrunun denklemi de şöyledir:
y-3=-2(x-1)
y-3=-2x+2
y+2x-5=0 olur.

güzel açıklamışsın tebrikler

Çok teşekkür ederim çok yardımcı oldunuz

C.3
2. sorunun çözümünde verdiğim formüle göre bu soru da çözülebilir. Bu soru için ek bilgi olarak eğimin doğrunun x ekseniyle pozitif yönde yaptığı açının tanjantına eşit olduğunu bilmemiz gerekiyordu.
Buna göre doğrunun eğimi=tan(30)=1/√3 olur.
Geçtiği noktada orjin noktası yani (0,0)'dır. Formüle göre doğrunun denklemi şu şekildedir:
y=(1/√3).x
İçler dışlar çarpımından da;
y√3=x buluruz.

Biz ama tan'a falan geçmedik o yüzden anlamdm

Peki, 30-60-90 özel üçgenini biliyor musunuz?

Evet onu biliyorm

Şöyle anlatıyım:
Doğrunun eğimi, bir doğrunun x ekseniyle pozitif yönde yaptığı açının tanjantıdır. Burada pozitif yönden kasıt, doğrunun x ekseniyle yaptığı iki açıdan sağda olanıdır.

Tanjant dediğimiz de dik üçgende açının karşısındaki kenarın uzunluğunun komşusundaki kenarın uzunluğuna oranıdır.

30-60-90 üçgenini düşünürsek de tan(30)=1/√3 olur.