S-1) Bir üçgen dik prizmanın taban ayrıtları 16 cm,10 cm ve 14 cm dir.Bir yan ayrıtı 5√3 cm olan bu prizmanın alanını bulunuz.
S-2) Düzgün altıgen dik prizmanın tabanının bir kenarı 4 cm, yanal alanı 192 cm² dir.Bu prizmanın yüksekliğini bulunuz.
S-3) Cisim köşegeni 12√3 alan küpün alanını bulunuz.
S-4) Bir küpün bir köşesinden geçen cisim köşegeninin, bu köşeden geçen ayrıtlarla belirttiği açıların birbirine eş olduğunu gösteriniz.
S-5) Bir dikdörtgenler prizmasının cisim köşegenlerinin uzunluklarının karelerinin toplamının, ayrıtlarının uzunluklarının karelerinin toplamına eşit olduğunu gösteriniz.
S-2) Düzgün altıgen dik prizmanın tabanının bir kenarı 4 cm, yanal alanı 192 cm² dir.Bu prizmanın yüksekliğini bulunuz.
S-3) Cisim köşegeni 12√3 alan küpün alanını bulunuz.
S-4) Bir küpün bir köşesinden geçen cisim köşegeninin, bu köşeden geçen ayrıtlarla belirttiği açıların birbirine eş olduğunu gösteriniz.
S-5) Bir dikdörtgenler prizmasının cisim köşegenlerinin uzunluklarının karelerinin toplamının, ayrıtlarının uzunluklarının karelerinin toplamına eşit olduğunu gösteriniz.
C-1) Üst ve alt üçgenlerin alanları eşit ve u'lu alan formülünden u=(10+14+16)/2=20
Üçgenin alanı=√20.(20-10).(20-14).(20-16)=40√3 .
Yanlardaki 3 dikdrötgenin alanı= 10.5√3+14.5√3+16.5√3=200√3
Tüm alan=2.40√3+200√3=280√3
C-2) Altıgen prizmada 6 tane yan dikdörtgen vardır. Bir tanesinin alanı 192/6=32 cm²
Bir dikdrötgenin alanı altıgenin bir kenarı çarpı yüksekliktir.
4.h=32 => h=8 cm dir.
C-3) Cisim köegeni küpte a.√3 ile bulunur.
a.√3=12.√3 ise
a=12 dür. Küpün alanı 6.a²= 6.12²=864
C-4)
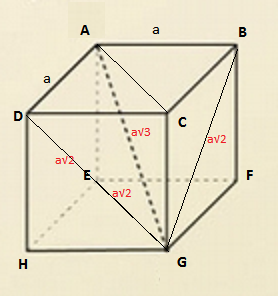
Not:Şekilde |EG| ve |DG| a√2 dir. ÜStüste geldiği için yalnış anlaşılmasın
[AG] cisim köşegenidir. A noktasında bahsedilen açıları yazalım.
Bahsettiği açılar; DAG, GAB, EAG açılarıdır. DAG, GAB, EAG üçgenlerinin kenarları incelendiğinde 3 üçgenin kenarları birbirine eştir. Bu 3 üçgenin kenar uzunlukları a, a√2, a√3 dür. Bu 3 üçgen eştir. Bu üç üçgendede DAG, GAB, EAG açıları hep a√2 olan kenarın karşısındadır. O zaman bu açılar eştir.
Ekstra olarak; bu açı x olsun. Bu açıyı bulmak için a, a√2, a√3 üçgeninde kosinüs teoremi yazılırsa cosx=1/√3 bulunur. Bu açıda x≈54,74⁰
C-5)
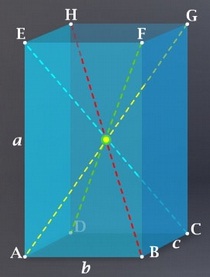
4 tane cisim köşegeni vardır.
Bir cisim köşegeni √a²+b²+c² ile bulunur. Bir cisim köşgeninin karesi a²+b²+c² dir. 4 cisim köşegeninin karelerinin toplamı 4.(a²+b²+c²) dır (1.)
12 tane ayrıtı vardır. Bunu 4 a , 4ü b, 4ü c dir. Bunların kareleri 4.a², 4b², 4c² dir. Bunların toplamı 4.a²+4b²+4c² dır (2.)
1. ile 2. eşittir. 4.(a²+b²+c²)=4.a²+4b²+4c²
Üçgenin alanı=√20.(20-10).(20-14).(20-16)=40√3 .
Yanlardaki 3 dikdrötgenin alanı= 10.5√3+14.5√3+16.5√3=200√3
Tüm alan=2.40√3+200√3=280√3
C-2) Altıgen prizmada 6 tane yan dikdörtgen vardır. Bir tanesinin alanı 192/6=32 cm²
Bir dikdrötgenin alanı altıgenin bir kenarı çarpı yüksekliktir.
4.h=32 => h=8 cm dir.
C-3) Cisim köegeni küpte a.√3 ile bulunur.
a.√3=12.√3 ise
a=12 dür. Küpün alanı 6.a²= 6.12²=864
C-4)

Not:Şekilde |EG| ve |DG| a√2 dir. ÜStüste geldiği için yalnış anlaşılmasın
[AG] cisim köşegenidir. A noktasında bahsedilen açıları yazalım.
Bahsettiği açılar; DAG, GAB, EAG açılarıdır. DAG, GAB, EAG üçgenlerinin kenarları incelendiğinde 3 üçgenin kenarları birbirine eştir. Bu 3 üçgenin kenar uzunlukları a, a√2, a√3 dür. Bu 3 üçgen eştir. Bu üç üçgendede DAG, GAB, EAG açıları hep a√2 olan kenarın karşısındadır. O zaman bu açılar eştir.
Ekstra olarak; bu açı x olsun. Bu açıyı bulmak için a, a√2, a√3 üçgeninde kosinüs teoremi yazılırsa cosx=1/√3 bulunur. Bu açıda x≈54,74⁰
C-5)

4 tane cisim köşegeni vardır.
Bir cisim köşegeni √a²+b²+c² ile bulunur. Bir cisim köşgeninin karesi a²+b²+c² dir. 4 cisim köşegeninin karelerinin toplamı 4.(a²+b²+c²) dır (1.)
12 tane ayrıtı vardır. Bunu 4 a , 4ü b, 4ü c dir. Bunların kareleri 4.a², 4b², 4c² dir. Bunların toplamı 4.a²+4b²+4c² dır (2.)
1. ile 2. eşittir. 4.(a²+b²+c²)=4.a²+4b²+4c²
hocam cok işime yaradı
allah razı olsun
allah razı olsun
Diğer çözümlü sorular alttadır.
Cisim Köşegeni Soruları Dikdörtgenler Prizması Soruları ve Çözümleri Küp Soruları Ve Çözümleri Küp Uzunluk Soruları ve Çözümleri Prizma Hacim Soruları Çözümleri Prizma Soruları Çözümleri Prizmada Uzunluk Çözümlü Sorular Prizmalar Hacim Soruları Çözümleri
Tüm Etiketler
Tüm Etiketler
