[kalakala]

[gereksizyorumcu]

1.
∀x>0 için e^x/x>e olduğunu göstermemiz yeterli
x=1 için e^x/x=e dir

0<x<1 için (e^x-ex) ifadesinin türevi alınırsa türevin negatif olduğu yani x=1 deki köke kadar hep azalan olduğunu anlarız yani x<1 için e^x-ex ifadesi azala azala 0 a kadar gelmiş demek ki x<1 için e^x>ex

benzer şekilde x>1 içinde bu türev hep pozitif olduğundan bundan sonra da hep artan olacağından x>1 için e^x>ex olduğunu buluruz ve istediğimizi göstermiş oluruz. x>0 için e^x>e.x

2.
parabolün türevi alınısa teğetin eğimi -2x bulunur
parabolün üzerindeki bir (x₀,1-x₀²) noktası için eğim -2x₀ olduğuna göre bu doğruların denklemini yazdığımızda
y+2x₀.x=x₀²+1 denklemini elde ederiz
böyle bir doğru da x ve y eksenlerini
x=(x₀²+1)/2x₀
y=x₀²+1
de keser üçgenin alanı da bu ikisini çarpımının yarısı yani
(x₀²+1)²/4x₀ olacağından min. üçgen alanı için bu ifadenin türevi alınıp sıfıra eşitlenirse
3x⁴+2x²-1=0 (türev tam bu değil tabi ki ** paydadaki ifadelrin önemi yok amacımız türevin payının sıfır olması)
(3x²-1).(x²+1)=0 , x²=1/3 veya x²=-1
x²=1/3 kökünü ele alıp x=*±1/√3 buluruz fakat negatif kök şekle uygun değil
x=1/√3 buluruz
buradan y=1-x²=1-1/3=2/3 bulunur , A=(1/√3,2/3)

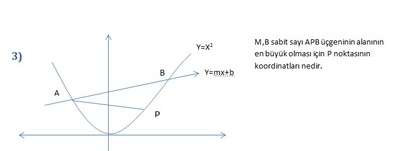
3.
bu soruyu farklı yollardan çözebiliriz ben A ve B noktaları sabit olduğuna göre P noktasının AB ye uzaklığını max. yapan P noktasına göre çözmeye çalışcağım ve bir yorum yapacağım P noktasındaki teğet kesen doğruya paralel olmak zorundadır. olaya tersinden baktığımızda AB ye en uzak P noktasını ardığımıza göre eğer doğruya paralel teğetin daha içindeki bir nokta olsa paralelin üzerindeki nokta daha uzak olacağından max. alan olma durumuyla çelişecektir yok eğer daha uzak olsa bu sefer de parabolün dışında kalacaktır...

P(t,t²) olsa , o noktadaki teğetin eğimi m=2t olmalıdır , ya da t=m/2
buradan P(m/2,m²/4) bulunur.

[Serkan A.]

Elinize sağlık hocam. Zahmet oldu.

[kalakala]

çok teşekkür ederim elinize saglık

[duygu95]

Optimizasyon 12.sınıf konularında var mı matematiksel programlama değil miydi optimizasyon ???