1) a/b = 2b/c = 4c/a
a +b+c=12
olduğuna göre a-b+c kaçtır?
A)0 B)5 C)6 D)9 E)12 Cevap:C
2) a sayısı 1 den büyük farklı bir pozitif tam sayıdır.
a3 + a2 tabanında yazılabilecek rakamları farklı en büyük üç basamaklı sayının rakamları toplamı, aşağıdakilerden hangisine daima tam olarak bölünür?
A)a+1 B)a2 + 2a C)a2+2a+2 D)a2-1 E)a2+a+1 Cevap:C
3) 1 den 10 a kadar numaralandırılmış olan 10 tane top üç farklı kutuya rastgele dağıtılıyor.
Bu dağıtma işleminde en az iki kutuda top olduğu bilindiğine göre, çift numaralı topların yalnız bir kutuya tek numaralı topların da diğer iki kutuya (bu iki kutunun her birinde en az bir tane top olacak şekilde) konulmuş olma olasılığı kaçtır?
A) 1/39 B)32/39 C)10/(39-1) D)30/(39-1) E)1/(310-1) Cevap: D
a +b+c=12
olduğuna göre a-b+c kaçtır?
A)0 B)5 C)6 D)9 E)12 Cevap:C
2) a sayısı 1 den büyük farklı bir pozitif tam sayıdır.
a3 + a2 tabanında yazılabilecek rakamları farklı en büyük üç basamaklı sayının rakamları toplamı, aşağıdakilerden hangisine daima tam olarak bölünür?
A)a+1 B)a2 + 2a C)a2+2a+2 D)a2-1 E)a2+a+1 Cevap:C
3) 1 den 10 a kadar numaralandırılmış olan 10 tane top üç farklı kutuya rastgele dağıtılıyor.
Bu dağıtma işleminde en az iki kutuda top olduğu bilindiğine göre, çift numaralı topların yalnız bir kutuya tek numaralı topların da diğer iki kutuya (bu iki kutunun her birinde en az bir tane top olacak şekilde) konulmuş olma olasılığı kaçtır?
A) 1/39 B)32/39 C)10/(39-1) D)30/(39-1) E)1/(310-1) Cevap: D
3.
tüm durumlar 10 tane top var 3^10 , istenmeyen durum (kutuların boş olduğu 3 tanedir)
90/3^10-3
3.30/3(3^9-1)
30/3^9-1
1 tek Top 4 tek Top 5 çift top
C(3,1).C(2,1).C(5,1) = 30 durum (C(3,1) ile çarpmamızın nedeni çift toplar için kutu seçtik)
2 tek Top 3 tek Top 5 çift top
C(3,1).C(2,1).C(5,2) = 10.6 => 60 durum
Toplamda 90 durum olur.
tüm durumlar 10 tane top var 3^10 , istenmeyen durum (kutuların boş olduğu 3 tanedir)
90/3^10-3
3.30/3(3^9-1)
30/3^9-1
1 tek Top 4 tek Top 5 çift top
C(3,1).C(2,1).C(5,1) = 30 durum (C(3,1) ile çarpmamızın nedeni çift toplar için kutu seçtik)
2 tek Top 3 tek Top 5 çift top
C(3,1).C(2,1).C(5,2) = 10.6 => 60 durum
Toplamda 90 durum olur.
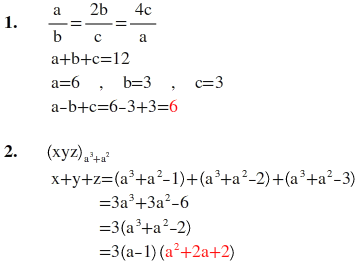
Çok teşekkür ederim. Hocam ilk soruyu değer vermeden yapmamızın bir yolu var mıdır?
Epey bir zaman geçmiş olmasına rağmen, belki bilmeyen birisi faydalanabilir.
İlk soruyu şöyle de çözebiliriz:
eşitliğini 2'li 2'li ele alıyoruz. Her bir eşitlik için içler dışlar çarpımı yapıyoruz.
a.c=2b² (I)
4.b.c=a² (II)
2.b.a=4.c² (III)
(I)'i (II)'ye bölüyoruz.
Gerekli sadeleştirmeyi yaptıktan sonra yine içler dışlar çarpımı yapıp sonucu:
a³=8.b³ buluyoruz.
(I)'i (III)'ye bölüyoruz.
Gerekli sadeleştirmeyi yaptıktan sonra yine içler dışlar çarpımı yapıp sonucu:
2.c³=2.b³ , c³=b³ buluyoruz.
(II)'i (III)'ye bölüyoruz.
Gerekli sadeleştirmeyi yaptıktan sonra yine içler dışlar çarpımı yapıp sonucu:
8.c³=a³ buluyoruz.
Sonuç olarak, bulduklarımızı değerlendirirsek,
c³=b³ ifadesinden c=b olur.
O zaman, 8.c³=a³ ifadesi ile a³=8.b³ ifadesinin aynı olduğu görülür, ve
2³.b³=a³ olur, buradan da 2.b=a olur.
Bize verilen a+b+c=12 ifade de bulduklarımızı yerine koyarsak
2.b+b+b=12
4.b=12 buradan b=3 bulunur.
b=c=3
a=2.b=2.3=6 olur.
Bizden a-b+c isteniyordu:
6-3+3=6 olarak buluruz.
İlk soruyu şöyle de çözebiliriz:
a
b
=
2.b
c
=
4
c
eşitliğini 2'li 2'li ele alıyoruz. Her bir eşitlik için içler dışlar çarpımı yapıyoruz.
a
b
=
2.b
c
a.c=2b² (I)
a
b
=
4
c
4.b.c=a² (II)
2.b
c
=
4
c
2.b.a=4.c² (III)
(I)'i (II)'ye bölüyoruz.
a.c
4.b.c
=
2.b²
a²
Gerekli sadeleştirmeyi yaptıktan sonra yine içler dışlar çarpımı yapıp sonucu:
a³=8.b³ buluyoruz.
(I)'i (III)'ye bölüyoruz.
a.c
2.b.a
=
2.b²
4.c²
Gerekli sadeleştirmeyi yaptıktan sonra yine içler dışlar çarpımı yapıp sonucu:
2.c³=2.b³ , c³=b³ buluyoruz.
(II)'i (III)'ye bölüyoruz.
4.b.c
2.b.a
=
a²
4.c²
Gerekli sadeleştirmeyi yaptıktan sonra yine içler dışlar çarpımı yapıp sonucu:
8.c³=a³ buluyoruz.
Sonuç olarak, bulduklarımızı değerlendirirsek,
c³=b³ ifadesinden c=b olur.
O zaman, 8.c³=a³ ifadesi ile a³=8.b³ ifadesinin aynı olduğu görülür, ve
2³.b³=a³ olur, buradan da 2.b=a olur.
Bize verilen a+b+c=12 ifade de bulduklarımızı yerine koyarsak
2.b+b+b=12
4.b=12 buradan b=3 bulunur.
b=c=3
a=2.b=2.3=6 olur.
Bizden a-b+c isteniyordu:
6-3+3=6 olarak buluruz.
