1-)

2-)

3-)


2-)
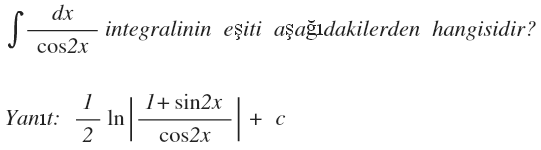
3-)

1
∫(cos^6x)+(sin^6x)dx dipnot: (a³+b³)=(a+b).(a²-ab+b²)
∫(cos²x)³+(sin²x)³dx
∫(cos²x+sin²x).(cos⁴x+sin⁴x-(sin²x.cos²x))dx
∫(1).((cos²x+sin²x)²-2.sin²x.cos²x)-(sin²x.cos²x))dx
∫(1).(1)-2.(sinx.cosx)²-(sinx.cosx)²)dx
∫1-3.(sinx.cosx)²dx
∫1-3.[(1/2).(sin2x)]²dx
∫1-3.[(1/4).(sin²(2x))]dx ----> cos4x=1-2sin²(2x) --> sin²(2x)=(1-cos4x)/2
∫1-(3/8).(1-cos4x)dx, nihayet integralden çıkaracağız:
x-(3/8).(x+(sin4x)/4)
(5x/8)-3.sin(4x)/32
∫(cos^6x)+(sin^6x)dx dipnot: (a³+b³)=(a+b).(a²-ab+b²)
∫(cos²x)³+(sin²x)³dx
∫(cos²x+sin²x).(cos⁴x+sin⁴x-(sin²x.cos²x))dx
∫(1).((cos²x+sin²x)²-2.sin²x.cos²x)-(sin²x.cos²x))dx
∫(1).(1)-2.(sinx.cosx)²-(sinx.cosx)²)dx
∫1-3.(sinx.cosx)²dx
∫1-3.[(1/2).(sin2x)]²dx
∫1-3.[(1/4).(sin²(2x))]dx ----> cos4x=1-2sin²(2x) --> sin²(2x)=(1-cos4x)/2
∫1-(3/8).(1-cos4x)dx, nihayet integralden çıkaracağız:
x-(3/8).(x+(sin4x)/4)
(5x/8)-3.sin(4x)/32
3
(t^6)=2x+1 -> x=[(t^6)-1]/2
6.t⁵dt=2dx, dx=3.t⁵dt
√(2x+1)=t³
∛(2x+1)=t²
[(t³-t²)/[(t^6)-1]/2].(3.t⁵dt)
6.(t⁵).(t³-t²)dt/((t^6)-1))
86.(t^8)-6.(t^7)]/[(t^6)-1]
(t^6)=2x+1 -> x=[(t^6)-1]/2
6.t⁵dt=2dx, dx=3.t⁵dt
√(2x+1)=t³
∛(2x+1)=t²
[(t³-t²)/[(t^6)-1]/2].(3.t⁵dt)
6.(t⁵).(t³-t²)dt/((t^6)-1))
86.(t^8)-6.(t^7)]/[(t^6)-1]
C-2)
tanx=t dönüşümü yaparsak, öncelikle dik üçgen yardımıyla cosx=1/√(t²+1) bulunur.
tanx=t ise (1+tan²x)dx=dt buradan dx=dt/(1+tan²x) bulunur. tanx=t idi o halde dx=dt(1+t²) oldu
cos2x=2cos²x-1=[2/(t²+1)]-1=(1-t²)/(t²+1) bulunur.
∫[dt.(1+t²)/(1+t²)]/(1-t²)=∫dt/(1-t²)
∫dt/(1-t²)=A/(1-t)+B/(1+t)
=(1/2).[ln(1-t)-ln(1+t)]+C
=1/2[ln[(1+tanx)/(1-tanx)]+C
tanx=t dönüşümü yaparsak, öncelikle dik üçgen yardımıyla cosx=1/√(t²+1) bulunur.
tanx=t ise (1+tan²x)dx=dt buradan dx=dt/(1+tan²x) bulunur. tanx=t idi o halde dx=dt(1+t²) oldu
cos2x=2cos²x-1=[2/(t²+1)]-1=(1-t²)/(t²+1) bulunur.
∫[dt.(1+t²)/(1+t²)]/(1-t²)=∫dt/(1-t²)
∫dt/(1-t²)=A/(1-t)+B/(1+t)
=(1/2).[ln(1-t)-ln(1+t)]+C
=1/2[ln[(1+tanx)/(1-tanx)]+C
Yazıyla ekleyebileceğiniz soruları resimle sormayınız.
Öncelikle çözümler için teşekkürler. Ama bu tarzda bir soruları lütfen benden yazıyla yazmamı beklemeyiniz. Site kurallarına elimden geldiğince uymaya çalışıyorum ama bu tarz sorularda hoşgörü gösteriniz lütfen. Diğer konularıma bakarsanız mümkün olduğunca yazıyla yazmaya çalıştığımı göreceksiniz. İyi günler dilerim.
Öncelikle çözümler için teşekkürler. Ama bu tarzda bir soruları lütfen benden yazıyla yazmamı beklemeyiniz. Site kurallarına elimden geldiğince uymaya çalışıyorum ama bu tarz sorularda hoşgörü gösteriniz lütfen. Diğer konularıma bakarsanız mümkün olduğunca yazıyla yazmaya çalıştığımı göreceksiniz. İyi günler dilerim.
Var olan kuralları uygulatıyorum.
