V₁=(3,4)
V₂=(5,12) VEKTÖRLERİ arasındaki açıyı ortalayan bir vektör v=(k,-1) olduğuna göre, k kaç birim olabilir? (cevap:-4/7)
V₂=(5,12) VEKTÖRLERİ arasındaki açıyı ortalayan bir vektör v=(k,-1) olduğuna göre, k kaç birim olabilir? (cevap:-4/7)
C-1
Vektörler (0,0) noktasından da geçtiği için birer doğru denklemi yazabiliriz.
V₁ için denklem,
4x=3y
4x-3y=0 olacaktır.
V₂ için denklem 12x=5y
12x-5y=0 olacaktır.
(k,-1) noktası açıortay doğrusu üzerinde olduğundan iki doğruya uzaklığı eşit olacaktır.
Bir Noktanın Bir Doğruya Olan Uzaklığı Formülü
V₁ için uzaklığı,
|4k+3|/5
V₂ için uzaklığı,
|12k+5|/13
İki uzaklığı birbirine eşitlersek,
5|12k+5|=13|4k+3|
Mutlak değerli denklemi çözersek,
Mutlak değeri 0 yapan sayılar -5/12 ve -9/12
k>-5/12 olursa ikisi de pozitif çıkar.
5.(12k+5)=13(4k+3)
8k-14=0
8k=14
k=7/4 olabilir.
-9/12<k<-5/12 olursa |12k+5| negatif, |4k+3| pozitif çıkar.
-5(12k+5)=13(4k+3)
112k=-64
k=-4/7 olabilir.
k<-9/12 olursa, ikisi de negatif çıkar.
-5(12k+5)=-13(4k+3)
k=7/4 ancak belirlediğimiz aralıkta değil ve zaten bu kökü bulmuştuk.
k'nın alabileceği iki değer 7/4 ve -4/7 dir.
Vektörler (0,0) noktasından da geçtiği için birer doğru denklemi yazabiliriz.
V₁ için denklem,
4x=3y
4x-3y=0 olacaktır.
V₂ için denklem 12x=5y
12x-5y=0 olacaktır.
(k,-1) noktası açıortay doğrusu üzerinde olduğundan iki doğruya uzaklığı eşit olacaktır.
Bir Noktanın Bir Doğruya Olan Uzaklığı Formülü
V₁ için uzaklığı,
|4k+3|/5
V₂ için uzaklığı,
|12k+5|/13
İki uzaklığı birbirine eşitlersek,
5|12k+5|=13|4k+3|
Mutlak değerli denklemi çözersek,
Mutlak değeri 0 yapan sayılar -5/12 ve -9/12
k>-5/12 olursa ikisi de pozitif çıkar.
5.(12k+5)=13(4k+3)
8k-14=0
8k=14
k=7/4 olabilir.
-9/12<k<-5/12 olursa |12k+5| negatif, |4k+3| pozitif çıkar.
-5(12k+5)=13(4k+3)
112k=-64
k=-4/7 olabilir.
k<-9/12 olursa, ikisi de negatif çıkar.
-5(12k+5)=-13(4k+3)
k=7/4 ancak belirlediğimiz aralıkta değil ve zaten bu kökü bulmuştuk.
k'nın alabileceği iki değer 7/4 ve -4/7 dir.
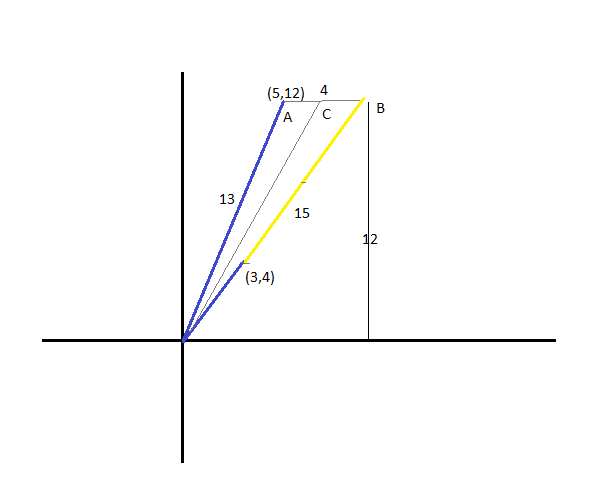
sayılar çok güzel olduğu için geometrik çözüm de yapabiliriz

(3,4) vektörünü 3 katına genişlettik yani (9,12) yaptık, bu işlemle açıortay değişmez
kenarları 13,4,15 olan üçgende açıortay teoremini yazarsak
AC/AB=13/15 ten
AC=13/7 bulunur
yani açıortayın eğimi 12/(5+(13/7))=7/4 olur (oluşturduğu diküçgenin kenarları 12 ve 13/7+5)
buradan da y değeri -1 ise
x değeri = k = -1/(7/4)=-4/7 bulunur
not: bana göre bu tek değerdir yani 7/4 bir çözüm değildir. tanım nasıl bilmiyorum ama 7/4 bunlar doğru olarak verilseydi çözümlerden biri olabilirdi ama vektörlerin arasında tek açıortay olduğunu düşünüyorum sonuçta iç bölgeleri belli
(3,4) vektörünü 3 katına genişlettik yani (9,12) yaptık, bu işlemle açıortay değişmez
kenarları 13,4,15 olan üçgende açıortay teoremini yazarsak
AC/AB=13/15 ten
AC=13/7 bulunur
yani açıortayın eğimi 12/(5+(13/7))=7/4 olur (oluşturduğu diküçgenin kenarları 12 ve 13/7+5)
buradan da y değeri -1 ise
x değeri = k = -1/(7/4)=-4/7 bulunur
not: bana göre bu tek değerdir yani 7/4 bir çözüm değildir. tanım nasıl bilmiyorum ama 7/4 bunlar doğru olarak verilseydi çözümlerden biri olabilirdi ama vektörlerin arasında tek açıortay olduğunu düşünüyorum sonuçta iç bölgeleri belli
Güzel çözümmüş hocam teşekkürler 
teşekkür ederim
teşekkürler
Bir çözüm de ben yazayım, lazım olur belki 
Açıortay doğrusunun eğimini bulunca soru bitiyor gibi.
(3,4) lük vektörün boyu 5 olduğu için, (5,12) lik vektörün boyunu 5 olacak şekilde kısaltalım. Bunun için (5,12) lik vektörü 5/13 ile genişletmemiz gerekir.
O zaman boyu 5 olan yeni vektörümüz (25/13 , 60/13 ) olur.
Şimdi bir ikizkenar üçgen elde ettik. İkizkenar üçgenin açıortayı, tabana diktir. sonucunu kullanırsak, (3,4) ve (25/13 , 60/13) vektörlerinin arasındaki eğim ile açıortayın eğimi birbirine diktir.
(3,4) ile (25/13 , 60/13 ) arasındaki eğim, -4/7 olduğundan açıortayın eğimi,
7/4 olur. k da, -4/7 olur.
Not, 7/4 bence de cevap değil.
Açıortay doğrusunun eğimini bulunca soru bitiyor gibi.
(3,4) lük vektörün boyu 5 olduğu için, (5,12) lik vektörün boyunu 5 olacak şekilde kısaltalım. Bunun için (5,12) lik vektörü 5/13 ile genişletmemiz gerekir.
O zaman boyu 5 olan yeni vektörümüz (25/13 , 60/13 ) olur.
Şimdi bir ikizkenar üçgen elde ettik. İkizkenar üçgenin açıortayı, tabana diktir. sonucunu kullanırsak, (3,4) ve (25/13 , 60/13) vektörlerinin arasındaki eğim ile açıortayın eğimi birbirine diktir.
(3,4) ile (25/13 , 60/13 ) arasındaki eğim, -4/7 olduğundan açıortayın eğimi,
7/4 olur. k da, -4/7 olur.
Not, 7/4 bence de cevap değil.
ABC üçgeninde ıBDı=2ıDCı, ıEAı=ıEBı
Verilenlere göre DE vektörünün AB ve AC vektörleri türünden ifadesi nedir?(cevap:AB-4AC/6)
