Soru 1
Samet ve Talat {1 , 2, 3, ...,10} kümesinin elemanları olan 10 tam sayıyı bir kağıda
yazıyorlar. Bu sayılardan herhangi ikisini silerek bunların yerine bu iki sayının toplamı ile elde edilen sayının rakamlar toplamını yazıyorlar. Bu işlem kağıtta bir sayı kalana kadar devam ediyor.
Buna göre kağıtta kalan sayı aşağıdakilerden hangisi olabilir ?
A)5 B)4 C)3 D)2 E)1
Soru 2
Samet ve Talat {1 , 2, 3, ...,10} kümesinin elemanları olan 10 tam sayıyı bir kağıda
yazıyorlar. Bu sayılardan herhangi ikisini silerek bunların yerine bu iki sayının toplamı ile elde edilen sayının rakamlar toplamını yazıyorlar. Bu işlem kağıtta bir sayı kalana kadar devam ediyor.
Buna göre kağıtta kalan sayı aşağıdakilerden hangisi olabilir ?
A)5 B)4 C)3 D)2 E)1
Soru 2
gereksizyorumcu 23:38 27 Şub 2015 #2
1.
bu soruda nasıl tek bir tane sayı geriye kalabilir? her adımda 2 sayı silinip 2 sayı yazılıyor.
eğer yalnızca toplam veya toplamın rakamlar toplamı yazılıyor ise
9 modunda yazılı sayıların toplam değeri hiç değişmeyeceğinden 1+2+...+9+10=55=1 mod9 olduğundan son kalan sayı 9 modunda 1e eşit olmalı
seçeneklerden 1 buna uygun.
2.
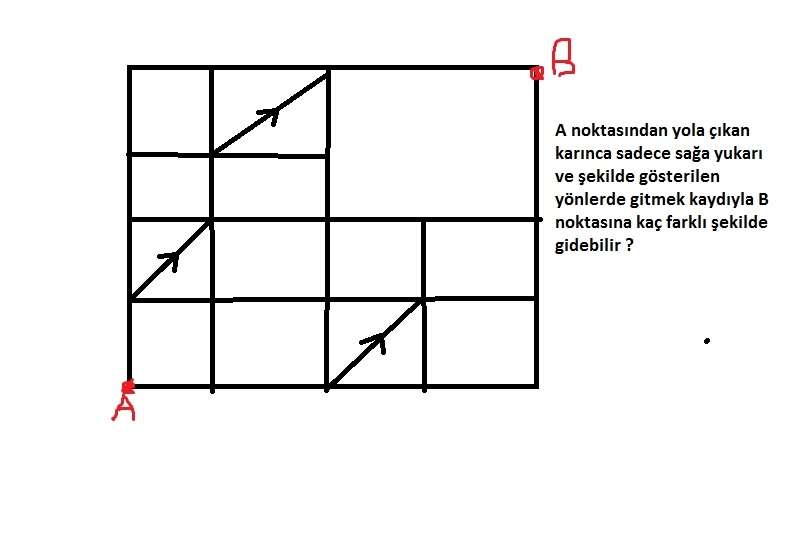
A köşesinden başlanıp her köşeye ona bağlantısı olan ve B ye giderken kendisinden geride olan köşelerin toplamını yaza yaza ilerlediğinizde (eğer yanlış yapmıyorsam) cevap 23+18=41 bulunuyor.
bu soruda nasıl tek bir tane sayı geriye kalabilir? her adımda 2 sayı silinip 2 sayı yazılıyor.
eğer yalnızca toplam veya toplamın rakamlar toplamı yazılıyor ise
9 modunda yazılı sayıların toplam değeri hiç değişmeyeceğinden 1+2+...+9+10=55=1 mod9 olduğundan son kalan sayı 9 modunda 1e eşit olmalı
seçeneklerden 1 buna uygun.
2.
A köşesinden başlanıp her köşeye ona bağlantısı olan ve B ye giderken kendisinden geride olan köşelerin toplamını yaza yaza ilerlediğinizde (eğer yanlış yapmıyorsam) cevap 23+18=41 bulunuyor.
İlgilendiğiniz için teşekkür ederim. 1. soruda soru metninde de belirtildiği üzere ikisi silinerek yerine ikisinin rakamlar toplamı yazılıyor. O yüzden gittiğiniz yol doğru. 2. sorunun cevabı da doğru ama mantığınızı tam anlayamadım. Mümkünse tekrar izah edebilir misiniz ? Tekrar teşekkür ederim.
gereksizyorumcu 23:57 28 Şub 2015 #4
telefondan flash desteği olmadığı için resim yükleyemiyorum, bilgisayarın başına geçtiğimde resim de yollamaya çalışırım
şimdilik açıklama yapmaya çalışırsak,
en agl satırdan soldan sağa doğru artacak şekilde köşe noktalarını numaralandırırsak (yani A noktası 1, en alt satırın en sağ noktası 5, içi boş karenin sol alt köşesi 13, sağ alt köşesi 15, sol üst köşesi 21 ve B noktası 22 numaralı noktalar olduğunda)
(köşe numarası, A noktasından o köşeye gidişlerin sayısı)
(1,1)-(2,1)-(3,1)-(4,1)-(5,1)-(6,1)-(7,2)-(8,3)-(9,5)-(10,6)
(11,1)-(12,4)-(13,7)-(14,12)-(15,18)-(16,1)-(17,5)-(18,12)-(19,1)-(20,6)-(21,23)-(22,41)
değerlerine ulaşılır.
örnek olarak 9 numaranın değerini 3,4 ve 8 numaralı noktaların değerleri toplamı oluşturuyor.
şimdilik açıklama yapmaya çalışırsak,
en agl satırdan soldan sağa doğru artacak şekilde köşe noktalarını numaralandırırsak (yani A noktası 1, en alt satırın en sağ noktası 5, içi boş karenin sol alt köşesi 13, sağ alt köşesi 15, sol üst köşesi 21 ve B noktası 22 numaralı noktalar olduğunda)
(köşe numarası, A noktasından o köşeye gidişlerin sayısı)
(1,1)-(2,1)-(3,1)-(4,1)-(5,1)-(6,1)-(7,2)-(8,3)-(9,5)-(10,6)
(11,1)-(12,4)-(13,7)-(14,12)-(15,18)-(16,1)-(17,5)-(18,12)-(19,1)-(20,6)-(21,23)-(22,41)
değerlerine ulaşılır.
örnek olarak 9 numaranın değerini 3,4 ve 8 numaralı noktaların değerleri toplamı oluşturuyor.
Anladım, resime gerek kalmadı. Çok teşekkür ederim, sağolun. Ancak konu kombinasyon olduğu için bunun acaba daha pratik bir yolu var mı diye düşünmeye başladım.