ne kadar uğraştıysam da upuzun işlem yapıyorum ama sonuca ulaşamıyorum 
svsmumcu26 23:25 12 Nis 2013 #2 C-3
Burada uzun bir şey yok aslında ya iç açıortayın boyu formülünden yada stewart teoreminden sonuca hemen ulaşabilirsiniz.
Ya da soldan 7 birimlik bir çıkıntı çekersiniz alt kısmı bulursunuz (İkizkenar stewart) yaparsınız.
Burada uzun bir şey yok aslında ya iç açıortayın boyu formülünden yada stewart teoreminden sonuca hemen ulaşabilirsiniz.
Ya da soldan 7 birimlik bir çıkıntı çekersiniz alt kısmı bulursunuz (İkizkenar stewart) yaparsınız.
svsmumcu26 23:29 12 Nis 2013 #3 C-1
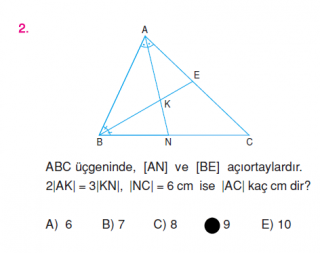
Burada |AK|=3K
|KN|=2K olsun.
|AB|=3k , |BN|=2k olur.
Şimdi diğer açı ortaydan
3k/2k = |AC|/6
18k=|AC|.2K
|AC|=9 br bulunur.
Burada |AK|=3K
|KN|=2K olsun.
|AB|=3k , |BN|=2k olur.
Şimdi diğer açı ortaydan
3k/2k = |AC|/6
18k=|AC|.2K
|AC|=9 br bulunur.
sentetikgeo 22:39 14 Nis 2013 #4
2)
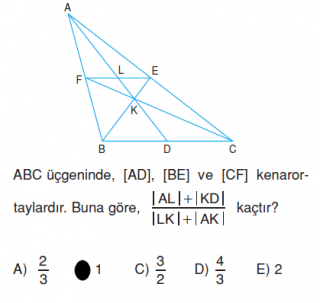
F ile D , E ile D birleştirilirse K noktası FED nin de ağırlık merkezi olacaktır. Çünkü [FE]//[BC] olduğundan [FL] [BD] nin , [LE] [DC] nin yarısı olacaktır. Zaten |BD|=|DC| idi. öyleyse |FL|=|LE| , Aynı durum FED nin diğer kenarları içinde geçerlidir. K'nın Hem FED'in Hem ABC nin ağırlık merkezi olduğunu gösterdik. |LK|=a , |KD|=2a , |AL|=3a .
3a+2a/a+4a=1.
Son yazdığım |LK|=a , |KD|=2a , |AL|=3a bir kuraldır. Belki bilmiyorsunuzdur diye ispatını da yaptım.
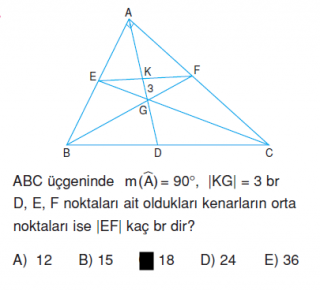
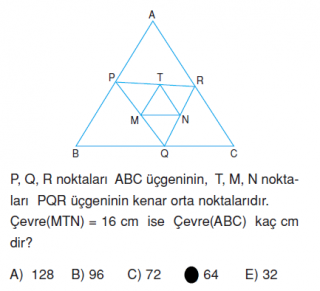
5)[MT]//[QR] , [TN]//[PQ] ve [MN]//[PR] aynı şekilde [QR]//[AB] , [PQ]//[AC] ve [PR]//[BC]
|MT|=a
|TN|=b
|MN|=c
|QR|=2a
|PQ|=2b
|PR|=2c
|AB|=4a
|AC|=4b
|BC|=4c
a+b+c=16 ise 4a+4b+4c=64
F ile D , E ile D birleştirilirse K noktası FED nin de ağırlık merkezi olacaktır. Çünkü [FE]//[BC] olduğundan [FL] [BD] nin , [LE] [DC] nin yarısı olacaktır. Zaten |BD|=|DC| idi. öyleyse |FL|=|LE| , Aynı durum FED nin diğer kenarları içinde geçerlidir. K'nın Hem FED'in Hem ABC nin ağırlık merkezi olduğunu gösterdik. |LK|=a , |KD|=2a , |AL|=3a .
3a+2a/a+4a=1.
Son yazdığım |LK|=a , |KD|=2a , |AL|=3a bir kuraldır. Belki bilmiyorsunuzdur diye ispatını da yaptım.
5)[MT]//[QR] , [TN]//[PQ] ve [MN]//[PR] aynı şekilde [QR]//[AB] , [PQ]//[AC] ve [PR]//[BC]
|MT|=a
|TN|=b
|MN|=c
|QR|=2a
|PQ|=2b
|PR|=2c
|AB|=4a
|AC|=4b
|BC|=4c
a+b+c=16 ise 4a+4b+4c=64
svsmumcu26 19:42 22 Haz 2013 #5
4.
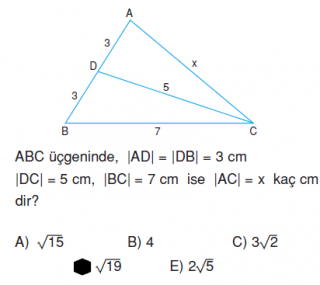
Burada aşağıdaki üçgene bakılırsa 3-5-7 üçgeni gereği 7ye bakan açı 120* olacaktır.
bütünleri olduğundan 180*-120*=60* sol alt açı olur.
şimdi 3-5-x üçgeni ve xi gören açı 60* olduğu bulunmuş oldu
x için kosinüs teoremi uygularsanız sonuca ulaşırsınız.
Burada aşağıdaki üçgene bakılırsa 3-5-7 üçgeni gereği 7ye bakan açı 120* olacaktır.
bütünleri olduğundan 180*-120*=60* sol alt açı olur.
şimdi 3-5-x üçgeni ve xi gören açı 60* olduğu bulunmuş oldu
x için kosinüs teoremi uygularsanız sonuca ulaşırsınız.