permütasyon

"Pascal toplamı" veya "köşe toplamı" şeklinde adlandırabileceğimiz metodla ilk 2 soru çözülmüştür:







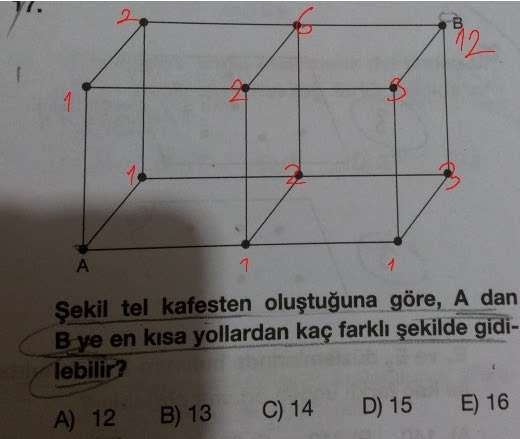
19 nolu üçgen sorusu:
Sağ kenar üzerinde 6 nokta var. Üçgenlerin hepsinin bir kenarı bu sağ kenar üzerinde olduğundan; C(6,2)=15 bulunur.

5 gül ve 6 karanfilden 1 gül ve bir karanfil C(5,1).C(6,1)=30 farklı şekilde seçilebilir.

Yol sorusu:
B'ye uğramadan en üstten gitse 7 farklı dönüş vardır, dolayısıyla alt yolu da hesaba katarsak 14.
B'ye uğrayarak gitse A ile B arası her yol için geri dönüş 8 şıklı-yollu; o zaman 3.8=24

Toplam=24+14=38 bulunur.

çok tşk ederm hocam..ama yol sorusunun cevabı 56..
bi de şu paskal köşe metodunu anlatsanz biraz soru üzerınde tam olarak anlayamadım

Köşe toplamını açıklar mısnız biraz

Ne yapalım 56 ise?.. İllâ 56 mı bulacağız yâni?!. Yanlış, hem de hokkalı yanlış. Soruyu şöyle çözmüşler:

2.3=6 ve bir de A'dan C'ye direkt 2 yol var toplamda 8 gidiş var demiş o zaman geriye 8-1=7 dönüş vardır demiş ve çarpmaya göre saymış 8.7=56 şeklinde bulmuşlar. Ama bu mantık tamamen yanlıştır. 6 yol ile 2 yol ayrıklar...


İstediğiniz açıklama. Sol alt köşeden, sağ üst köşeye giden (en kısa) yolların toplam sayısı. 8x8'lik bir bir yolda gösterilmiştir:


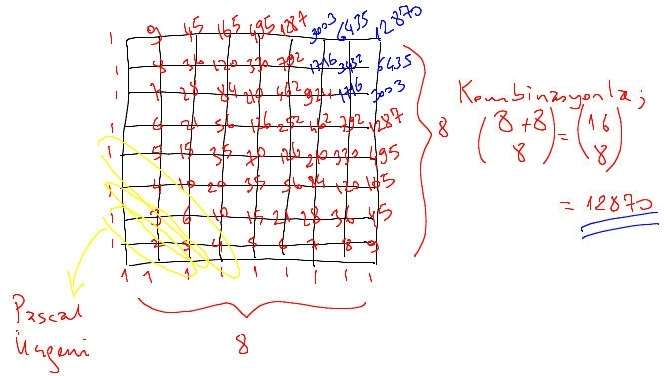
Ayrıca buraya bakınız. "Pascal" formatında yazılmış kelimelerin kaç farklı okunabileceğine dair:
https://www.matematiktutkusu.com/for...syon-trig.html (Int.permütasyon.trig.)