Merkezi eğilim ölçüleri: Ortanca (medyan), Tepe değeri(mod) ve Aritmetik ortalamadır.
Merkezi yayılım ölçüleri: Standart Sapma, Açıklık (aralık), çeyrekler açıklığıdır.
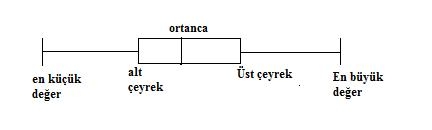
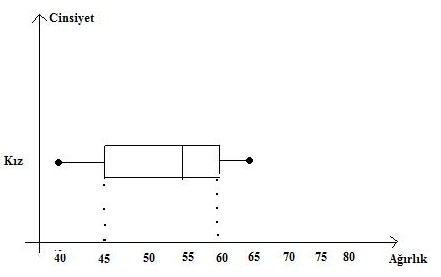
Ortanca (medyan): Küçükten büyüğe veya büyükten küçüğe doğru sıralanmış bir dağılımı tam ortadan ikiye bölen değerdir. Ölçümlerin yarısı bu değerin üstünde, diğer yarısı bu değerin altında yer alır.
Tepe Değeri (mod): Veri grubu küçükten büyüğe doğru sıralandığında en çok tekrar eden sayı tepedeğerdir (mod). Tepedeğer birden fazla olabilir.
Aritmetik Ortalama: Veri grubundaki tüm sayılar toplanıp veri sayısına bölünürse artimetik ortalama bulunur.
Açıklık(Aralık): En büyük değer ile en küçük değerin arasındaki fark açıklıktır.
Çeyrekler Açıklığı: Üst çeyrekle alt çeyrek arasındaki fark çeyrekler açıklığıdır.
Standart Sapma :
Standart sapma bulunurken.
*Önce verilen dizinin aritmetik ortalaması bulunur.
*Her bir veri ile aritmetik ortalama arasındaki fark bulunur.
*Bulunan farkların her birinin karesi alınır. Karelerden elde edilen sayılar toplanır.
*Bulunan toplam veri sayısının 1 eksiğine bölünür ve elde edilen bölümün karekökü alınırsa standart sapma bulunmuş olur.
Z ve T puanlarının hesaplanması:
z puanı
z=Dönüştürülecek puan−Aritmetik OrtalamaStandart Sapma
formülü ile bulunur.
z puanından T puanına geçiş T=10z+50 formulü ile bulunur.
Konuyla ilgili ayrıntılı döküman için buraya bakınız.