Şimdiden herkese çok teşekkür ederim 





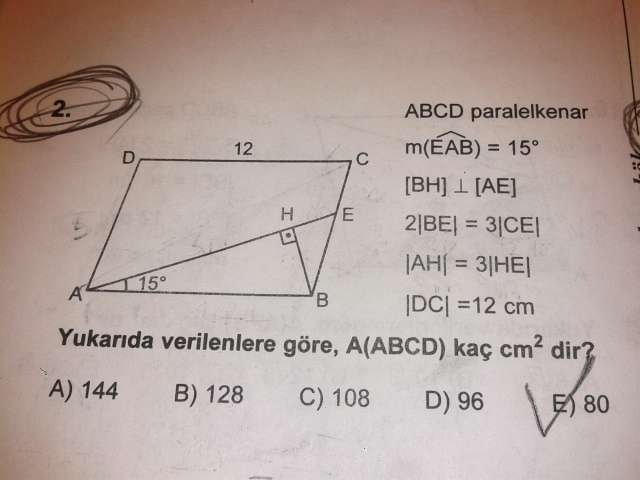

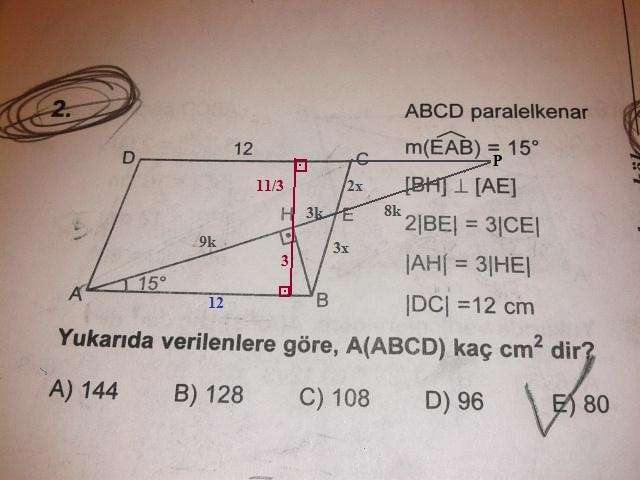
Paralelkenarın yüksekliğini çizersek, H noktasından AB ye inen kısım 3 cm olur. (15-75-90 üçgeni)
Daha sonra şekildeki gibi E ve C noktalarından çizip P de birleştirirsek, 3ün 2 ye oranı olduğundan |AE|=12k kabul edilirse |EP|=8k olur.
Bunu bulduktan sonra yüksekliğe geçersek 9un 11 e oranından yükseklik 3 e 11/3 gelir. Toplam yükseklik 20/3 olur.
Paralelkenarın alanı=20/3.12=80 olur.

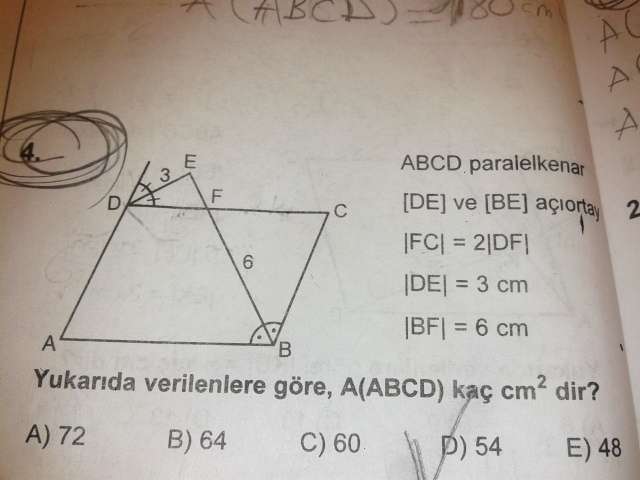
Açıortaylar orta taban üzerinde dik kesişirler. A köşesinden BE ye açıortayı çizersek diklik oluşur. Buna göre DE de BE ye diktir.
Daha sonra DEF ile altta oluşan dik üçgenin benzerliğinden AFB üçgeninin yüksekliği 9 bulunur.
Paralelkenarın alanı= 2A(AFB)=2.9.6/2=54

Şekildeki gibi oranları yazarsak;
A(KLM)=2k.3h/2=15 k.h=5 oluyor.
A(ABCD)=4k.4h=16.k.h.=80

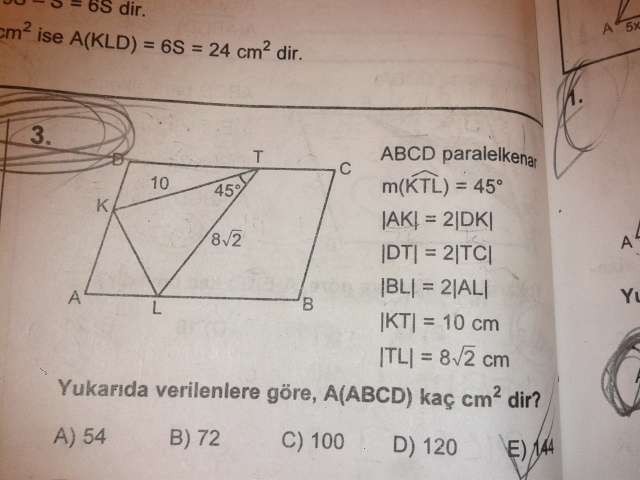
A(AKL)=k.2h/2=k.h=S dersek;
A(KDT)=2k.h/2=k.h.=S
A(TCBL)=(3k/2).3h=9k.h/2=9S/2
A(ABCD)=3k.3h=9S
A(KTL)=5S/2 oluyor.
5S/2=40
S=16
9S=144

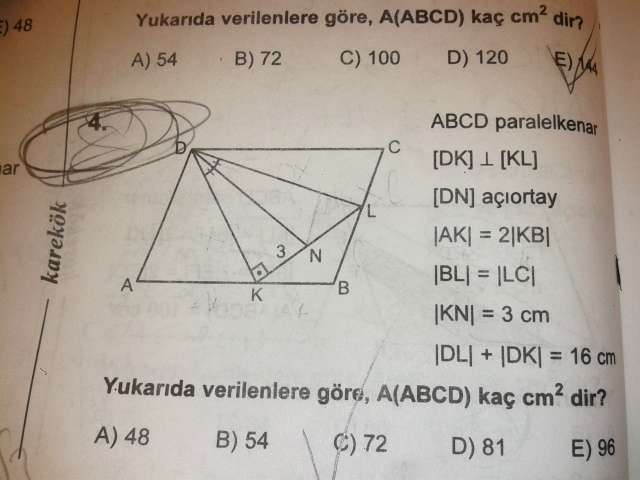
Paralelkenarda tüm iç açıların sinüsleri birbirine eşit olduğundan ve bu sinüs değerine t dersek;
A(DCL)=3x.k.t/2=3S
A(ADK)=2k.2x.t/2=4S
A(KBL)=k.x.t/2=S
A(ABCD)=3x.2k.t=12S
A(DKL)=4S oluyor.
A(DKL)=16.3/2=24=4S (Açıortaydan kenarlara çizilen dikmeler eşittir.)
S=6
12S=72 olur.
Hocam çok teşekkür ederim çözümler harika 
