1 sin²(3x+10)+sin²(2x+50)=1 denklemini sağlayan değerler?
2 Bir ABC üçgeninin kenar uzunlukları sırasıyla a, b, c dir. a=4b ve tanA=3tanB olduğuna göre cosA/cosB=? (4/3)
3

2 Bir ABC üçgeninin kenar uzunlukları sırasıyla a, b, c dir. a=4b ve tanA=3tanB olduğuna göre cosA/cosB=? (4/3)
3
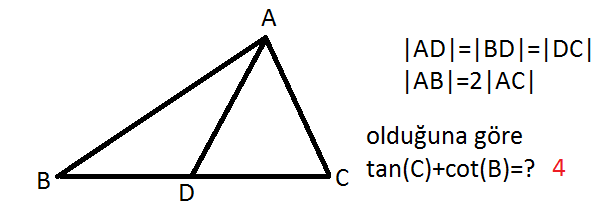
1.soru
formüller;
sin(90+x)=cosx
cos(90+x)=-sinx
cos²x+sin²x=1
çözüm;
sin²(3x+10)+sin²(2x+50)=1
iki sin ifadeyi cos şeklinde yaz. her biri için ayrı.
1.durum
sin²(3x+10)+sin²(2x-40+90)=1 yukarıdaki dönüşüm formüllerinden
sin²(3x+10)+cos²(2x-40)=1
cos²+sin²=1 durumu sadece açıları eş ise gerçeklerşir. o halde
3x+10=2x-40
x=-50
2.durum
sin²(3x-80+90)+sin²(2x+50)=1
cos²(3x-80)+sin²(2x+50)=1
3x-80=2x+50
x=130 gelir.
formüller;
sin(90+x)=cosx
cos(90+x)=-sinx
cos²x+sin²x=1
çözüm;
sin²(3x+10)+sin²(2x+50)=1
iki sin ifadeyi cos şeklinde yaz. her biri için ayrı.
1.durum
sin²(3x+10)+sin²(2x-40+90)=1 yukarıdaki dönüşüm formüllerinden
sin²(3x+10)+cos²(2x-40)=1
cos²+sin²=1 durumu sadece açıları eş ise gerçeklerşir. o halde
3x+10=2x-40
x=-50
2.durum
sin²(3x-80+90)+sin²(2x+50)=1
cos²(3x-80)+sin²(2x+50)=1
3x-80=2x+50
x=130 gelir.
3.soru 
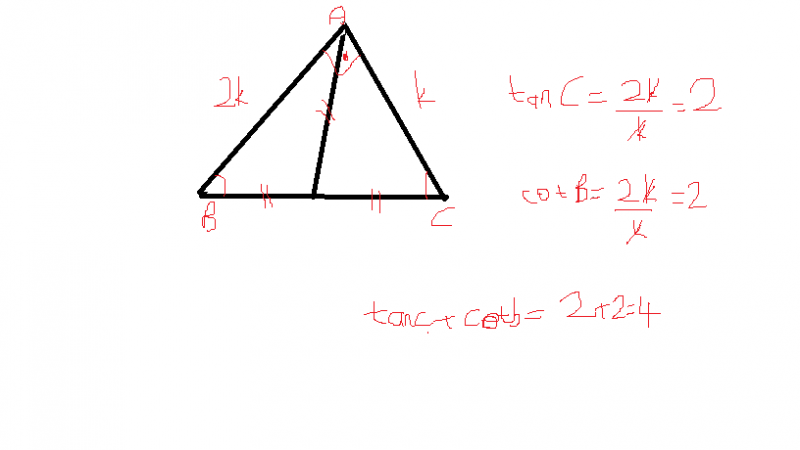
1.soru
formüller;
sin(90+x)=cosx
cos(90+x)=-sinx
cos²x+sin²x=1
çözüm;
sin²(3x+10)+sin²(2x+50)=1
iki sin ifadeyi cos şeklinde yaz. her biri için ayrı.
1.durum
sin²(3x+10)+sin²(2x-40+90)=1 yukarıdaki dönüşüm formüllerinden
sin²(3x+10)+cos²(2x-40)=1
cos²+sin²=1 durumu sadece açıları eş ise gerçeklerşir. o halde
3x+10=2x-40
x=-50
2.durum
sin²(3x-80+90)+sin²(2x+50)=1
cos²(3x-80)+sin²(2x+50)=1
3x-80=2x+50
x=130 gelir.
formüller;
sin(90+x)=cosx
cos(90+x)=-sinx
cos²x+sin²x=1
çözüm;
sin²(3x+10)+sin²(2x+50)=1
iki sin ifadeyi cos şeklinde yaz. her biri için ayrı.
1.durum
sin²(3x+10)+sin²(2x-40+90)=1 yukarıdaki dönüşüm formüllerinden
sin²(3x+10)+cos²(2x-40)=1
cos²+sin²=1 durumu sadece açıları eş ise gerçeklerşir. o halde
3x+10=2x-40
x=-50
2.durum
sin²(3x-80+90)+sin²(2x+50)=1
cos²(3x-80)+sin²(2x+50)=1
3x-80=2x+50
x=130 gelir.
Hocam sizin gibi yapınca
sina=cos(90-a)
1.durum
sin²(3x+10)+cos²(40-2x)=1
5x=30
x=6 geliyor.
2.durum
cos²(80-3x)+sin²(2x+50)=1
5x=30
x=6 geliyor.
benim merak ettiğim bu köklerin daha büyüklerini nasıl buluruz?
teşekkürler
sina=cos(90-a)
bu köklerin daha büyüklerini nasıl buluruz? neyi kastetdiniz? derece olarak mı daha büyük yoksa sayısal olarak mı daha büyük?
bu ifade yalnızca a=450 iken doğru.
bu köklerin daha büyüklerini nasıl buluruz? neyi kastetdiniz? derece olarak mı daha büyük yoksa sayısal olarak mı daha büyük?
bu köklerin daha büyüklerini nasıl buluruz? neyi kastetdiniz? derece olarak mı daha büyük yoksa sayısal olarak mı daha büyük?
sin3x=1/2 olsun x'in değerleri sorulsun. sin 30 ve 150 için 1/2 olur. buradan x=10 ve x=50 gelir bunları 120'şer olarak arttırsak gene denklem sağlanıyor yani 10,130,250 ve 50,170,290(0,2pi aralığı için). bunları denersek denklemin sağlandığını görebiliriz. burada 6 dan başka kök yok mu demek istiyorum. yani varsa da büyük vardır herhalde
hayır hocam yalnızca a=45 için doğru değil. sin0=cos90, sin30=cos60 gibi değerlerini bildiğimiz örnekleri hatırlayınız.
sin3x=1/2 sorusunda evet 120 ekleyerek hangi aralıkta ise o aralığa bağlı kalarak cevaplar bulunur. sonuçta
sin30=sin150=...=1/2
ama yukarıdaki soruda x değerlerini arttırırsanız içler aynı olmayabilir.
