Arkadaşlar Rasyonel Sayılar neden sayılamaz ? ve Reel sayılar neden sayılabilir ? Bunun ispatı isteniyor ne şekilde açıklayabilirim bu durumu ?
bi klavye sürçmesi olmuş sanırım.
rasyonel sayılar sayılabilir (countable) reel sayılar ise sayılamaz (uncountable).
forumda ikisi için de ispat paylaşıldı diye hatırlıyorum ama yanılıyor olabilirim siz bi aratın cantor falan diye bişey bulamazsanız bilgisayar başına geçince yardımcı olmaya çalışayım.
rasyonel sayılar sayılabilir (countable) reel sayılar ise sayılamaz (uncountable).
forumda ikisi için de ispat paylaşıldı diye hatırlıyorum ama yanılıyor olabilirim siz bi aratın cantor falan diye bişey bulamazsanız bilgisayar başına geçince yardımcı olmaya çalışayım.
bi klavye sürçmesi olmuş sanırım.
rasyonel sayılar sayılabilir (countable) reel sayılar ise sayılamaz (uncountable).
forumda ikisi için de ispat paylaşıldı diye hatırlıyorum ama yanılıyor olabilirim siz bi aratın cantor falan diye bişey bulamazsanız bilgisayar başına geçince yardımcı olmaya çalışayım.
rasyonel sayılar sayılabilir (countable) reel sayılar ise sayılamaz (uncountable).
forumda ikisi için de ispat paylaşıldı diye hatırlıyorum ama yanılıyor olabilirim siz bi aratın cantor falan diye bişey bulamazsanız bilgisayar başına geçince yardımcı olmaya çalışayım.
Teşekkürler.
olabilir muhtemelen defterinize yazarken bir hata olmuştur, neyse mühim değil.
yöntemler biraz daha görsellik (ya da açıklama) gerektirdiğinden link vereyim , eğer ingilizceniz varsa ingilizce kaynaktan okumanızda da fayda var
http://tr.wikipedia.org/wiki/Cantor'un_köşegen_yöntemi
Cantor's diagonal argument - Wikipedia, the free encyclopedia
burada reel sayıların doğal sayılarla birebir eşleşemeyeceğinin yani reel sayıların sayılamaz olduğunun ispatını bulabilirsiniz.
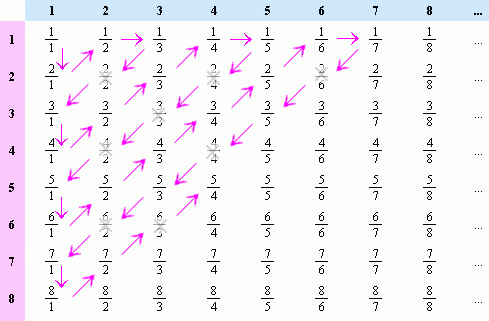
google da yaptığımız bir aramada hemen karşımıza çıkan şu resimdeyse tüm rasyonel sayıların elbet listede bir yerde çıkacağını ve dolayısıyla sayılabilir (doğal sayılarla eşleştirilebilir) olduğunu görmüş oluyoruz

eğer sayılabilir kümelerin kartezyen çarpımlarının sayılabilir olduğunu söyleyen teoremi biliyorsak rasyonel sayıların sayılabilir olduğunu
(p/q) rasyonel sayısını (p,q) noktasına eşleştirerek ve p ve q nun tamsayı olup sayılabilir kümelerin elemanı olmasından hareketle de söyleyebiliriz.
yöntemler biraz daha görsellik (ya da açıklama) gerektirdiğinden link vereyim , eğer ingilizceniz varsa ingilizce kaynaktan okumanızda da fayda var
http://tr.wikipedia.org/wiki/Cantor'un_köşegen_yöntemi
Cantor's diagonal argument - Wikipedia, the free encyclopedia
burada reel sayıların doğal sayılarla birebir eşleşemeyeceğinin yani reel sayıların sayılamaz olduğunun ispatını bulabilirsiniz.
google da yaptığımız bir aramada hemen karşımıza çıkan şu resimdeyse tüm rasyonel sayıların elbet listede bir yerde çıkacağını ve dolayısıyla sayılabilir (doğal sayılarla eşleştirilebilir) olduğunu görmüş oluyoruz
eğer sayılabilir kümelerin kartezyen çarpımlarının sayılabilir olduğunu söyleyen teoremi biliyorsak rasyonel sayıların sayılabilir olduğunu
(p/q) rasyonel sayısını (p,q) noktasına eşleştirerek ve p ve q nun tamsayı olup sayılabilir kümelerin elemanı olmasından hareketle de söyleyebiliriz.
