1) Rakamları farklı 6 basamaklı 2a7b1c doğal sayısının 4 ile bölümünden kalan 3'tür. Bu sayı 11 ile tam böülünüyor. Buna göre, a kaç farklı değer alabilir? (Ben 2 değer buldum 4 ve 8) Cevap:1 miş
2) Rakamları farklı 6 basamaklı 11 ile tam bölünebilen en büyük doğal sayının 5 ile bölümündeki kalan kaçtır? (cevap 0)
3) c<b<a olmak üzere 9 ve 5 ile bölündüğünde 3 kalanını veren üç basamaklı kaç tane abc sayısı yazılabilir?
4) a,b,c pazitif tamsayılardır. a nın b ye bölümünde bölüm c , kalan c dir.
a nın alabileceği farklı değerlerin toplamı 84.b olduğuna göre , b kaçtır?
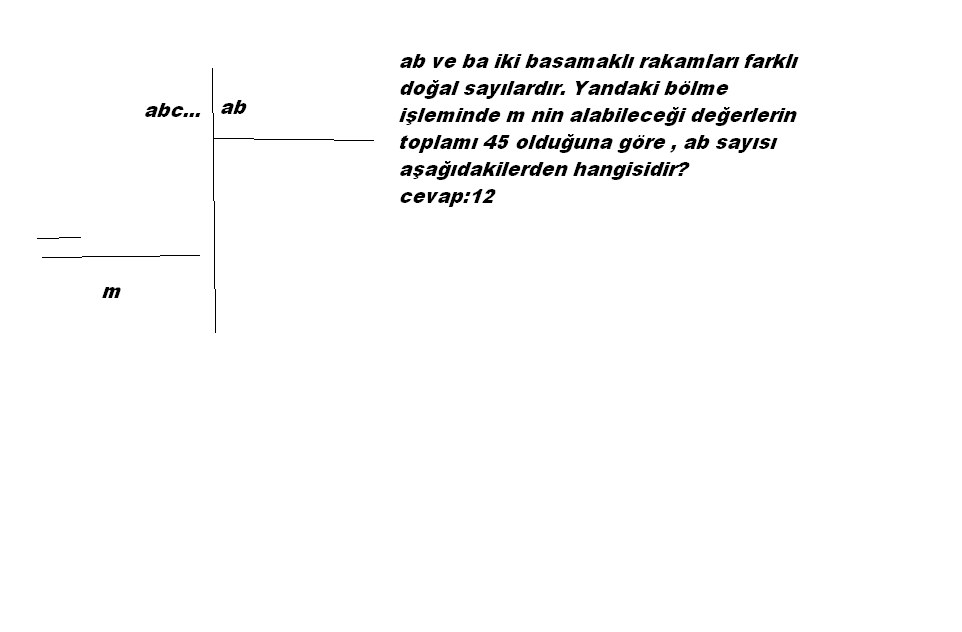
5)
2) Rakamları farklı 6 basamaklı 11 ile tam bölünebilen en büyük doğal sayının 5 ile bölümündeki kalan kaçtır? (cevap 0)
3) c<b<a olmak üzere 9 ve 5 ile bölündüğünde 3 kalanını veren üç basamaklı kaç tane abc sayısı yazılabilir?
4) a,b,c pazitif tamsayılardır. a nın b ye bölümünde bölüm c , kalan c dir.
a nın alabileceği farklı değerlerin toplamı 84.b olduğuna göre , b kaçtır?
5)
2)
İlk önce en büyük basamak değerlerine en büyük rakamları vererek işe başlarsak sayımız:
987654 olur.
(4+6+8≠5+7+9). Burada birler basamağı 7 olursa ancak sayı 11 ile tam bölünebilir; fakat sorudaki rakamları farklı şartına uymadığı için çare onlar basamağını değiştirmekte aranır. Yeni sayı:
987646 olmalı ki sayı 11 ile tam bölüne bilsin. Rakamları farklı şartını yeniden sağlamadığı için hem birler, hem onlar basamağında değişiklik yaparsak sayı:
987635 olur. (5+6+8=3+7+9). Sayı 11 ile tam bölünebilir ve birler basamağı 5 olduğundan beş ile bölümünden kalan 0 dir.
İlk önce en büyük basamak değerlerine en büyük rakamları vererek işe başlarsak sayımız:
987654 olur.
(4+6+8≠5+7+9). Burada birler basamağı 7 olursa ancak sayı 11 ile tam bölünebilir; fakat sorudaki rakamları farklı şartına uymadığı için çare onlar basamağını değiştirmekte aranır. Yeni sayı:
987646 olmalı ki sayı 11 ile tam bölüne bilsin. Rakamları farklı şartını yeniden sağlamadığı için hem birler, hem onlar basamağında değişiklik yaparsak sayı:
987635 olur. (5+6+8=3+7+9). Sayı 11 ile tam bölünebilir ve birler basamağı 5 olduğundan beş ile bölümünden kalan 0 dir.
*imza
sanırım noktalar beyaz. zekice.
sanırım noktalar beyaz. zekice.
Emin olmamakla beraber:


1. sorunun cevabını 6 buldum.
C.3
abc=9x+3=5y+3
abc-3=okek(9,5)=45k
abc=45k+3
k=12 için abc=543
C.3
abc=9x+3=5y+3
abc-3=okek(9,5)=45k
abc=45k+3
k=12 için abc=543
@sinavkizi
Çok doğru.
Çok doğru.
4) a=bc+c=c(b+1) ............(1)
c<b olmalı ayrıca c nin alacağı değerler 1,2,3,...,b-1 olabilir bunları teker teker (1) nolu ifadede yazıp toplayın böylece
(b+1)+2(b+1)+3(b+1)+...+(b-1)(b+1)=84b
(b+1)(1+2+3+.....+b-1)=84b
(b+1)(b-1).b/2=84b
(b-1)(b+1)=2.84
(b-1)(b+1)=12.14
b=13 olur
5)yukarıdaki çözüme benzer mantıkla siz yapabilirsiniz
c<b olmalı ayrıca c nin alacağı değerler 1,2,3,...,b-1 olabilir bunları teker teker (1) nolu ifadede yazıp toplayın böylece
(b+1)+2(b+1)+3(b+1)+...+(b-1)(b+1)=84b
(b+1)(1+2+3+.....+b-1)=84b
(b+1)(b-1).b/2=84b
(b-1)(b+1)=2.84
(b-1)(b+1)=12.14
b=13 olur
5)yukarıdaki çözüme benzer mantıkla siz yapabilirsiniz
1) sayılar 247819 ve 287419 şeklinde 2 farklı a sayısı olur çözüm 1 zaten olamaz a ve b değeri bulunup bunların yaptığımız gibi simetriğini alarak ikinci çözümü yazarız
teşekkürler aerturk hocam ve furkan elinize sağlık
1. sorunun cevabını 6 buldum.
C.3
abc=9x+3=5y+3
abc-3=okek(9,5)=45k
abc=45k+3
k=12 için abc=543
C.3
abc=9x+3=5y+3
abc-3=okek(9,5)=45k
abc=45k+3
k=12 için abc=543
çözüm kısa görünüyor ama 12 yi nasıl bulduğunu da açıklaman gerek tek tek değer vermek zor olmaz mı
