1)
∞∑n=03^nn!toplamının değeri kaçtır?
A)0 B)1 C)3 D)e3 E)∞
2)
∞∑k=51+2+3+..+(k-1)k.k!ifadesinin değeri kaçtır?
A)1/24 B)1/36 C)1/42 D)1/48 E)1/60
3) 1,2,2,3,3,3,4,4,4,4,.....,100,100,100(100tane) sonlu dizisinin 2005. elemanı aşağıdakilerden hangisidir?
A)61 B)62 C)63 D)64 E)65
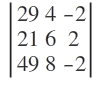
4)
determinantının değeri kaçtır?
A)6 B)4 C)2 D)1 E)0
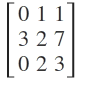
5)
|Ek(A).A| determinantının değeri kaçtır?
A)0 B)6 C)-12 D)-18 E)-27