C
Kusura bakmayın. MEBin Tabletinden yazıyorum o yüzden şekil eklyemedim. Çözüm şöyle:
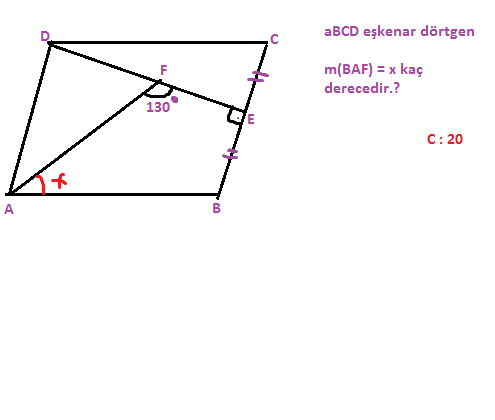
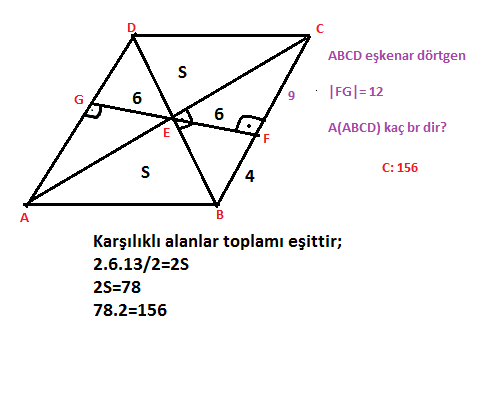
CE=EB=a dersek eşkenar dörtgenden dolayı DC=2a olur. Şimdi DCE dik üçgenine bakalım. Dik kenarlarından biri a ve hipotenüsü 2a olduğuna göre C açısı 60 olmalı. C 60'sa B açısı da 120 olur(paralellik). Şimdi de AFEB dörtgenine bakalım. İç açıları toplmının 360 olması için A açsı 20 olmalı.
Kusura bakmayın. MEBin Tabletinden yazıyorum o yüzden şekil eklyemedim. Çözüm şöyle:
CE=EB=a dersek eşkenar dörtgenden dolayı DC=2a olur. Şimdi DCE dik üçgenine bakalım. Dik kenarlarından biri a ve hipotenüsü 2a olduğuna göre C açısı 60 olmalı. C 60'sa B açısı da 120 olur(paralellik). Şimdi de AFEB dörtgenine bakalım. İç açıları toplmının 360 olması için A açsı 20 olmalı.
Teşekkür ederim.
Diğer sorularımı da çözebilecek arkadaşlar aranıyor
Diğer sorularımı da çözebilecek arkadaşlar aranıyor
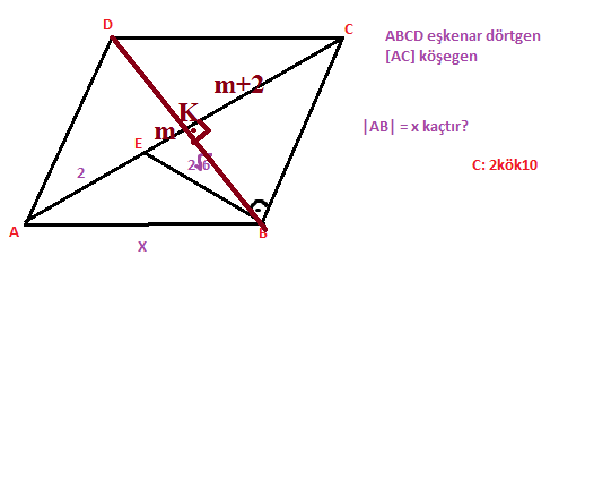
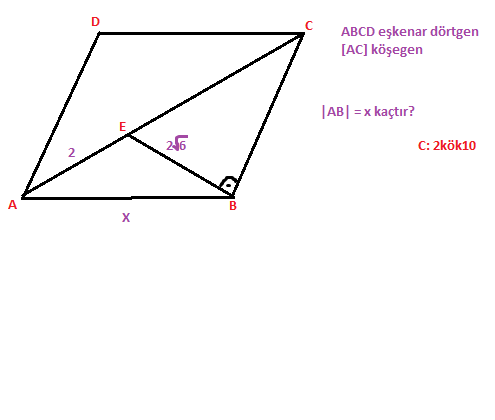
Eşkenar dörtgenin diğer köşegenini çizersek kuraldan dolayı mevcut köşegene dik olacaktır. Ve yine kuraldan eşkenar dörtgenin iki köşegeni birbirini ortalayacaktır. Bundan dolayı kenar uzunlukları şekildeki m,m+2 gibi olur. Şimdi de BCE üçgeninde öklit bağıntısnı uygularsak; KB²=m²+2m olur. Şimdi de BEK üçgeninde pisagor uyguyalalım. 2m²+2m=(2√6)²=24 olur. Her tarafı 2 ile bölelim.
m²+m=12 olur. Sol tarafı m parantezine alalım. m(m+1)=12 olur ki buradan m=3 olur. Şimdi de AKB üçgeninde pisagor uygularsak; x²=40 olur. Buradan x=2√10
Teşekkür ederim arkadaşlar.
Son sorum kaldı
Son sorum kaldı
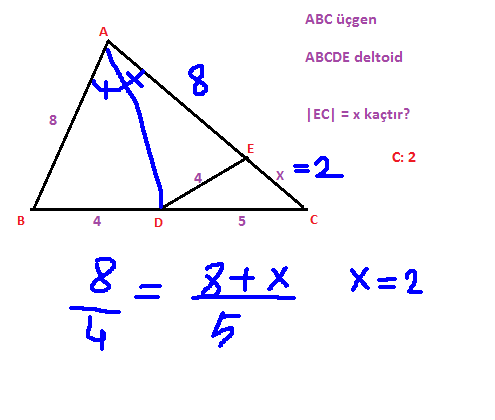

Sağolun arkadaşlar 
