1 
olduğuna göre 3x-2y+1=0 koşulunu sağlayan kaç tane y tam sayısı vardır? [ÇÖZÜLDÜ]
2
olmak üzere
2x-y+4=0 olduğuna göre, y nin alabileceği tam sayı değerlerinin toplamı kaçtır? [ÇÖZÜLDÜ]
3 y bir asal sayı olmak üzere, Recep misketlerini y li ve y+2 li gruplara ayırdığında her seferinde 5 misketi artıyor.
Recep' in 260 tan az misketi olduğu bilindiğine göre, en fazla kaç misketi olabilir?
4 a ve b birer tam sayıdır.
2a+b sayısının 8 ile bölümünden kalan 5 olduğuna göre, 6a+21b sayısının 12 ile bölümünden kalan kaçtır? [ÇÖZÜLDÜ]
5 x ve y birer tam sayıdır.
2x+3y sayısının 5 ile bölümünden kalan 4 olduğuna göre, 8x+7y sayısının 5 ile bölümünden kalan kaçtır? [ÇÖZÜLDÜ]
[1-9] [2-68] [3-257] [4-9] [5-1]
Teşekkürler
olduğuna göre 3x-2y+1=0 koşulunu sağlayan kaç tane y tam sayısı vardır? [ÇÖZÜLDÜ]
2
olmak üzere2x-y+4=0 olduğuna göre, y nin alabileceği tam sayı değerlerinin toplamı kaçtır? [ÇÖZÜLDÜ]
3 y bir asal sayı olmak üzere, Recep misketlerini y li ve y+2 li gruplara ayırdığında her seferinde 5 misketi artıyor.
Recep' in 260 tan az misketi olduğu bilindiğine göre, en fazla kaç misketi olabilir?
4 a ve b birer tam sayıdır.
2a+b sayısının 8 ile bölümünden kalan 5 olduğuna göre, 6a+21b sayısının 12 ile bölümünden kalan kaçtır? [ÇÖZÜLDÜ]
5 x ve y birer tam sayıdır.
2x+3y sayısının 5 ile bölümünden kalan 4 olduğuna göre, 8x+7y sayısının 5 ile bölümünden kalan kaçtır? [ÇÖZÜLDÜ]
[1-9] [2-68] [3-257] [4-9] [5-1]
Teşekkürler
sentetikgeo 14:24 08 Tem 2013 #2
1)
svsmumcu26 14:27 08 Tem 2013 #4
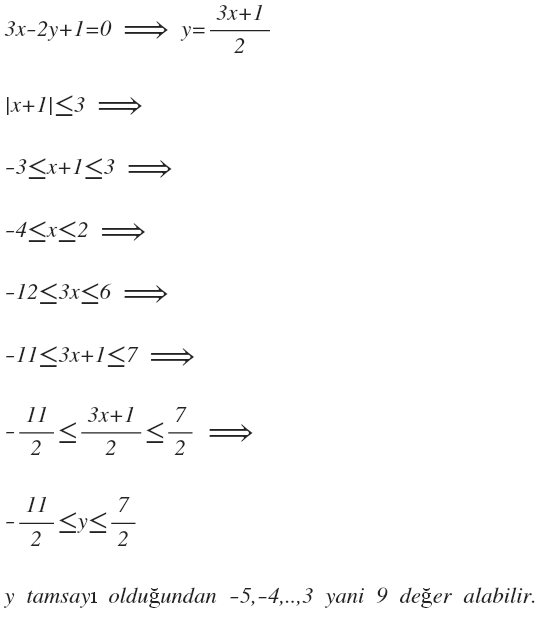
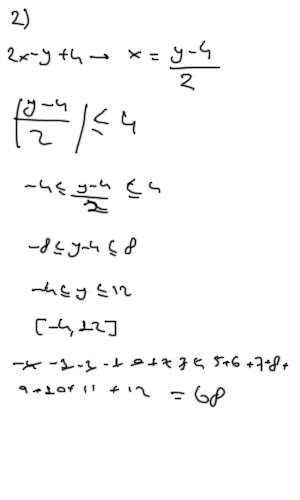
Arkadaşlar soruları resimle çözmek yerine,editörle çözerseniz çok daha iyi olur zira bu görüntüler ilerde kendiliğinden silinebilmektedir.
@sentetikgeo 2. soruyu da aynı yolla çözdüm teşekkürler
*istanbuL. saolasın kardeşim
*istanbuL. saolasın kardeşim
sentetikgeo 14:31 08 Tem 2013 #6
5)
2x+3y sayısı ile 8x+7y sayısının toplamı 10x+10y yani 5'e bölünür.
Öyleyse 2x+3y 4 kalanını veriyorsa 8x+7y 1 kalanını verir.
2x+3y sayısı ile 8x+7y sayısının toplamı 10x+10y yani 5'e bölünür.
Öyleyse 2x+3y 4 kalanını veriyorsa 8x+7y 1 kalanını verir.
sentetikgeo 14:49 08 Tem 2013 #7
4)
6a+21b sayısı 3'e bölünür.
4'e bölümünden kalanı bulalım.
6a≡2a
21b≡b
Yani 6a+21b sayısının 4'e bölümünden kalan 2a+b sayısının 4'e bölümünden kalana eşittir.
2a+b sayısın mod8'de 5'denk ise mod4'de de 5'e denktir.
6a+21b sayısı 4'e bölününce 5 kalanını veriyor ve 3'e bölünüyorsa bu sayı 12'ye bölününce kaç kalanını verir acaba?
6a+21b=12k+n olsa
n sayısı 3'e bölünecek ve mod4'de 5'e denk olacak. Bu sayı 9'dur.
6a+21b sayısı 3'e bölünür.
4'e bölümünden kalanı bulalım.
6a≡2a
21b≡b
Yani 6a+21b sayısının 4'e bölümünden kalan 2a+b sayısının 4'e bölümünden kalana eşittir.
2a+b sayısın mod8'de 5'denk ise mod4'de de 5'e denktir.
6a+21b sayısı 4'e bölününce 5 kalanını veriyor ve 3'e bölünüyorsa bu sayı 12'ye bölününce kaç kalanını verir acaba?
6a+21b=12k+n olsa
n sayısı 3'e bölünecek ve mod4'de 5'e denk olacak. Bu sayı 9'dur.
3. soruya yardım edebilecek var mı
sentetikgeo 22:01 08 Tem 2013 #9
3)
Recep'in misket sayısı okek(y,y+2)+5 olacak.
y asal sayı olduğundan ekok(y,y+2)=y(y+2)
öyleyse Recep'in misketleri sayısı y(y+2)+5 olacak.
bu sayının büyük olması için y büyük olmalı fakat 260'ı da geçmemeli.
y=13 olursa 13.15+5=200<260
y=17 olursa 17.19+5=328>260
Yani en çok 200 olur.
Recep'in misket sayısı okek(y,y+2)+5 olacak.
y asal sayı olduğundan ekok(y,y+2)=y(y+2)
öyleyse Recep'in misketleri sayısı y(y+2)+5 olacak.
bu sayının büyük olması için y büyük olmalı fakat 260'ı da geçmemeli.
y=13 olursa 13.15+5=200<260
y=17 olursa 17.19+5=328>260
Yani en çok 200 olur.
Teşekkürler Emir