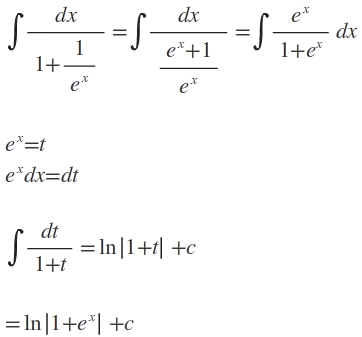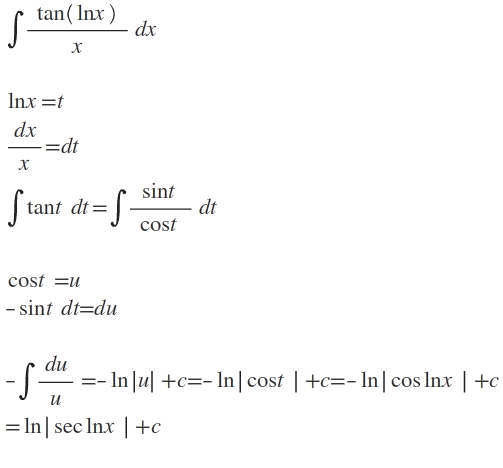1) (-1,3) ve (6,-4) noktalarından geçen doğru y=a/x-1 egrisine teğet olduğuna göre a kaçtır? 1/4
2) bir kenarı y=8 doğrusu üzerinde diğer iki köşesi de y=x³ ve y=-x³ eğrileri üzerinde olan ve Ox ekseninin üst tarafında kalan bölgeye cizilebilecek en büyük alanlı dikdortgenin uzun kenarı kaç birimdir? 6.
3) ∫ dx/ 1+ e^-x integralinin değeri nedir? ln|1+e^x| +c
4) ∫ [tan|lnx| / x] . dx integralinin eşiti nedir? ln|sec|lnx||+c
5) ∫ ln (x+2) dx integralinin eşiti nedir? (x+2). [ln|x+2|-1] +c