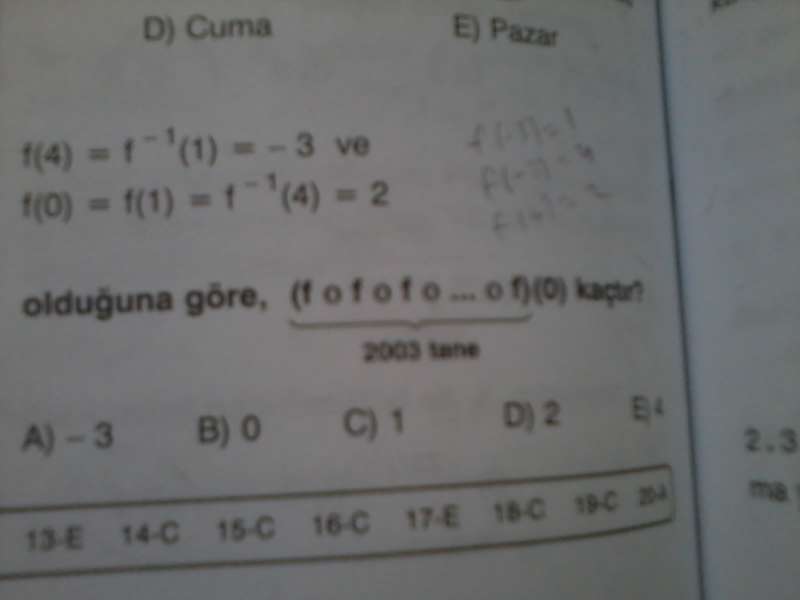1) Z/7 de, f(3x+4)=2x+5 olduğuna göre, f⁻¹(x) nedir?
cevap: 5x
2) (628+1327+1428+2227)50! sayısının 5 ile bölümünden kalan kaçtır?
cevap: 1
3) (111)¹¹¹+(222)²²²+(333)³³³+...+(999)999 toplamının 6 ile bölümünden kalan kaçtır?
cevap: 11
4)
cevap: 2004
5)
cevap: −3