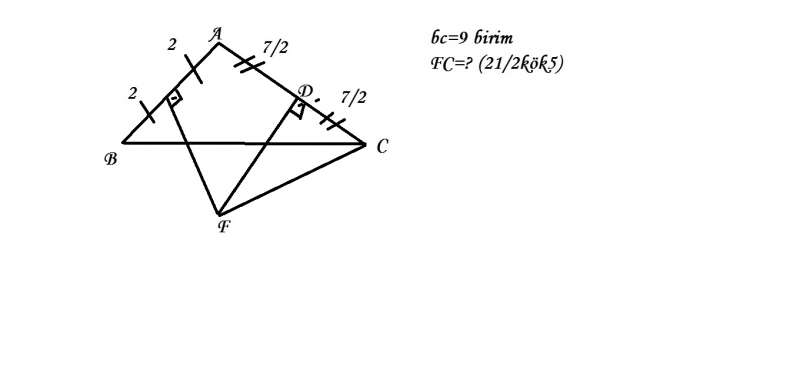
Merhabalar,
1 A=(1,2,3) ve B=(-2,-1,3,5) ise A'dan B'ye tanımlanabilecek fonksiyon olmayan bağıntı sayısı kaçtır? (2^12)-(4^3)
2 f: R->R ve -3≤x<5 ve f(x)=3x-6 fonksiyonunun görüntü kümesinde kaç tane tam sayı vardır? (24)
3 f(x.)=f(x)+f(y) ve f(3)=(1/3) ise f(3^15)=? (5)
4 f(x)=(x+2m)/(1-(2/x)) şeklinde tanımlanan f(x) fonksiyonu birim fonksiyon ise m=? (-1)
5 f(x)=(m-2)x²+nx+k+1 fonksdiyonu verliyor. f(2x-3) fonksiyonu birim fonksiyonsa m+n+k=? (2 ama 0 buluyorum)
6 f(x)=(x-1)/(x+1) ise f(2x)'in f(x) türünden eşiti nedir? [3f(x)+1]/[f(x)+3]
7 f(x)= |x+4|+√(x-3) ise f(19)+f⁻¹(27)=? (46)
8 f(x) doğrusal fonksiyondur.
fof(x)=9x ise (fofof)(4) kaç olabilir? (108)
9 (sorunun tümü hatrımda değil ama geldiğim yeri ve cevap seçeneğini doğru hatırlıyorum
tan2x=2 ise tan²x=? (2)
10 Bu sorunun cos teoremi ve çemberden yararlanmak dışında başka bir çözümü var mı diye merak ediyorum: