1) Rakamları farklı 6 basamaklı 2a7b1c doğal sayısının 4 ile bölümünden kalan 3'tür. Bu sayı 11 ile tam böülünüyor. Buna göre, a kaç farklı değer alabilir? (Ben 2 değer buldum 4 ve 8) Cevap:1 miş
2) Rakamları farklı 6 basamaklı 11 ile tam bölünebilen en büyük doğal sayının 5 ile bölümündeki kalan kaçtır? (cevap 0)
3) c<b<a olmak üzere 9 ve 5 ile bölündüğünde 3 kalanını veren üç basamaklı kaç tane abc sayısı yazılabilir?
4) a,b,c pazitif tamsayılardır. a nın b ye bölümünde bölüm c , kalan c dir.
a nın alabileceği farklı değerlerin toplamı 84.b olduğuna göre , b kaçtır?
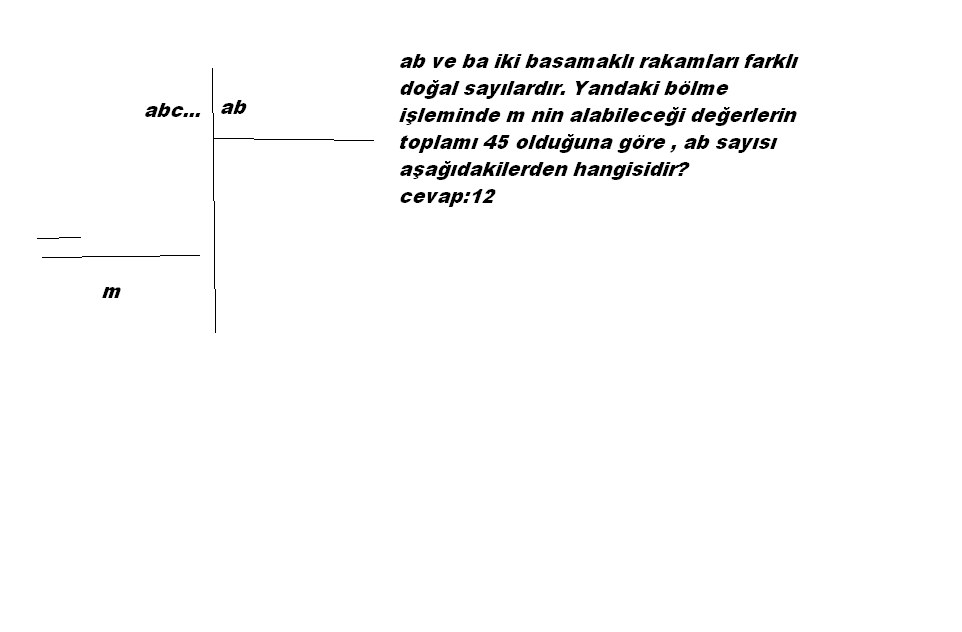
5)