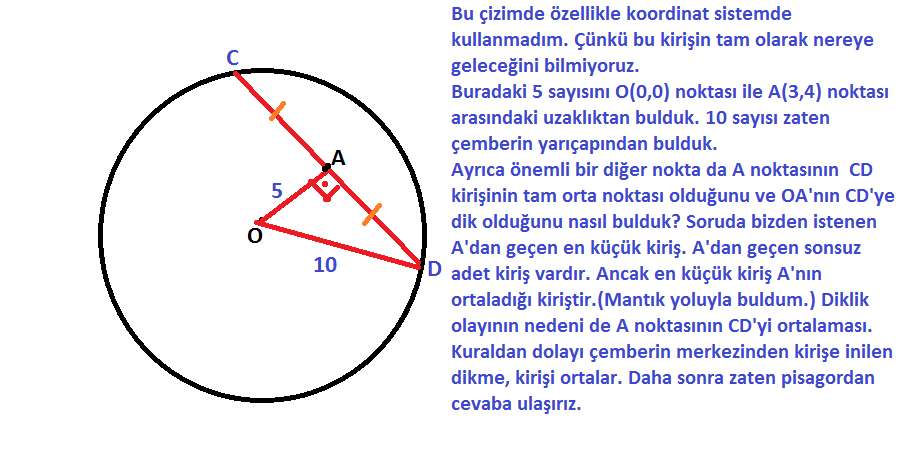
1. Analitik düzlemde x²+y²=100 denklemi ile verilen çemberin içindeki A(3,4) noktasından geçen en kısa kirişin uzunluğu kaç birimdir? (10√3)
2. Analitik düzlemde x²+y²-8x+6y-75=0 denklemi ile verilen çembere dıştan teğet ve yarıçapı 2 br olan çemberlerin merkezlerinin geometrik yerinin denklemi nedir? ((x-4)²+(y+3)²=144
3. Anal. düzlemde verilen (x-2)²+(y-3)²=16 çemberinin orijin merkezli ve k=3 oranlı homotetiğinin denklemi nedir? ((x-6)²+(y-9)²=144
4. Anal. düzlemde verilen x²+y²-2x+4y+1=0 çemberinin u=(5,6) vektörü doğrultusunda ötelenmesi ile elde edilen çember denklemi nedir? (x-6)²+(y-4)²=4